Paper
A unifying mutual information view of metric learning: cross-entropy vs. pairwise losses
Recently, substantial research efforts in Deep Metric Learning (DML) focused on designing complex pairwise-distance losses, which require convoluted schemes to ease optimization, such as sample mining or pair weighting. The standard cross-entropy loss for
arxiv.org
Code
github.com/jeromerony/dml_cross_entropy
jeromerony/dml_cross_entropy
Code for the paper "A unifying mutual information view of metric learning: cross-entropy vs. pairwise losses" (ECCV 2020 - Spotlight) - jeromerony/dml_cross_entropy
github.com
Introduction
겉으로 보기에는 standard cross-entropy loss와 DML에서 쓰이는 pairwise loss들이 관계가 없어 보인다.
본 논문에서는 실제로는 이 두가지 loss가 관련이 있으며 'MI'(mutual-information)을 통해서 살펴보면 둘다 MI를 최대화하는 방향으로 학습을 시키는 것을 알 수 있다. 그래서 MI를 기반으로 pairwise loss들과 cross-entropy loss는 서로 관련이 있으며 cross-entropy loss는 MI측면에서 upper bound임을 증명한다.
Summary of contributions
1. DML loss들의 관계 및 learned feature와 labels에 대한 MI의 generative view를 정립하였다.
2. standard cross-entropy를 최적화하는 것은 pairwise loss의 bound-optimizer를 approximation하는 것이다. (?)
3. 좀더 제너럴한 뷰에서, standard cross-entropy loss는 discriminative한 뷰에서 feature와 labels간의 MI를 최대화하는 것과 같다.
4. 위와 같은 내용을 실험을 통해 증명하였다.

On the two view of the mutual information
Mutual information은 2개의 random variable이 공유하는 information량을 측정하는 수학적 식이다.
본 논문에서는 learned feature Z와 label Y의 MI를 계산한다. 이때 MI는 대칭이기 때문에 2가지 view로 살펴볼 수 있다.
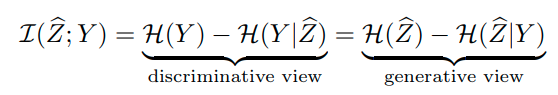
MI를 maximize 하기 위해서 discriminative view 관점에서 보면
label은 balanced되어 있어야 하고, ( H(Y)값 최대) feature가 condition으로 주어진 상황에서는 entropy가 작은, 즉 Y label이 잘 구분되어야 한다. 이와 다르게 generative view는 embedding space상 feature는 최대한 퍼져있어야 하지만 label이 주어졌을 때 feature는 최대한 뭉쳐있어야 함을 의미한다.
이때, discriminative view는 label identification에 집중되어 있고, generative view는 learned feature에 집중되어 있다.
이는 label 중심의 cross-entropy loss와 feature중심의 feature-shaping loss과의 관계를 분석할 수 있다.
Pairwise losses and the generative view of the MI
Pairwise loss들은 , generative view에서 mutual information을 maximization하는 형태로 해석될 수 있다.
1) The example of contrastive loss
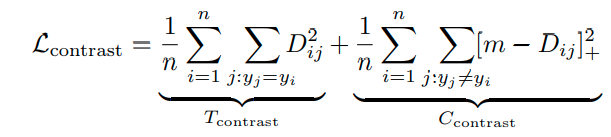
contrastive loss부터 분석을 시작해보자. contrastive loss는 첫번째 항처럼 i,j간의 거리를 줄여주는 term과 ij간의 거리를 특정 margin 이상은 유지하도록 하는 term으로 구성되어 있다. 첫번째 term은 같은 class의 sample간의 거리를 줄여주는 tightness part이고, 두번째 term은 다른 class의 sample 간의 거리를 유지해주는 contrastive part이다.


이때, T_contrast는 다음과 같이 conditional cross entropy로 해석될 수 있다.

이때, center loss 형태이기 때문에 다음과 같이 conditional distribution은 gaussian 분포를 따르게 된다.
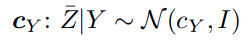
이때, T_constant는 다음과 같이 mutual information의 upper bound라고 해석될 수 있다.

이때, Z바|Y는 normal distribution을 따르기 때문에 아래와 같이 Z hat이 normal distribution을 따르면, 이와 같이 tight한 bound를 형성할 수 있고, T_contrast를 minimizing하는 것은 H(Z_hat|Y)를 minimizing하는 것과 같다. 이는 Y가 주어졌을때 Z_hat에 대한 entropy값을 줄이는 것이므로 각 cluster에 대해 feature가 뭉치도록 embedding 시킨다는 것과 같다.
그러나 이러한 형태로 optimization을 진행하는 경우, 모든 data point를 한 곳에 mapping시키는 trivial encoder를 만들어낼 가능성이 있다. 또한 이것이 global optimum이기도 하다.
이러한 trivial solution을 막기 위해서, second term이 필요하다. 그리고 이 second term이 contrastive term이다.
이 term은 아래와 같이 구성된다.
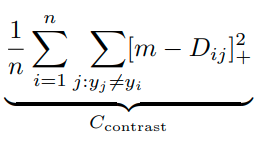
그렇기 때문에 D_ij가 m보다 작을때, cost가 발생하고, x를 아래와 같이 정의할때,

다음과 같은 appoximation을 이용해서 식을 고칠 수 있다.
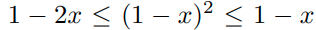

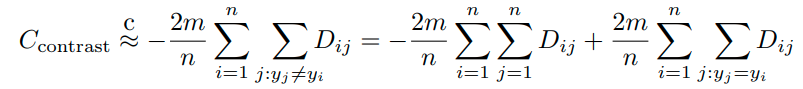
이 식에서 두번째 term은 tightness objective를 만족하기에 충분하다.
첫번째 term은 differential entropy estimator로 해석이 가능하다.

2가지 term 모두 Z-hat의 퍼진 정도를 측정한다. 결론적으로 contrastive loss를 minimizing하는 것은 label Y와 embedded feature Z_hat의 MI를 최대화하는 것의 proxy로 해석할 수 있다.

2) Generalizing to other pairwise losses
다른 pairwise loss들도 이와 유사하게 분석이 가능하다.


Cross-entropy does it all
Cross-entropy loss의 경우 위와 같이 tightness part와 contrastive part로 나뉘어지지 않는 것으로 보인다.
(unary classification loss)
그러나 실제로는 cross-entropy 또한 tightness part와 contrastive part로 나누어 생각할 수 있으며, pairwise loss와 똑같이 MI를 maximization하는 형태로 생각할 수 있다.
아래는 이에 대한 수학적 분석인데, 일단은 생략.. (논문 참고)
1) The pairwise loss behind unary cross-entropy
...
2) A discriminative view of mutual information
...
3) Then why would cross-entropy work better?
저자는 왜 cross-entropy loss와 pairwise loss가 동등하게 MI를 최대화하는 한다고 볼 수 있는데
cross-entropy loss가 더 좋은 성능을 보이는지 간단하게 설명하고 있다.
요약하자만 pairwise loss의 경우, pair를 잘 선정해야 되는 문제에서 부터 다소 복잡한 learning 과정을 수행하는데 반면에 cross-entropy loss는 간단한 형태로 진행되기 때문이라고 말하고 있다.