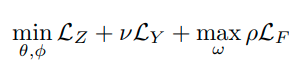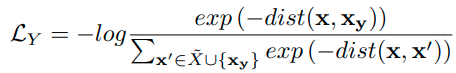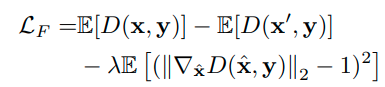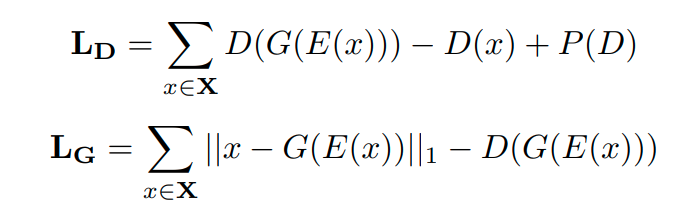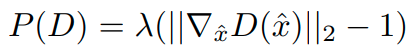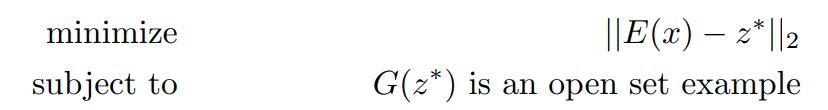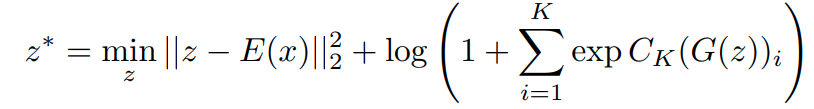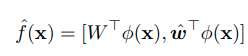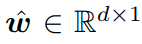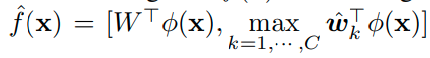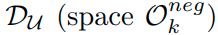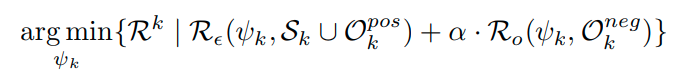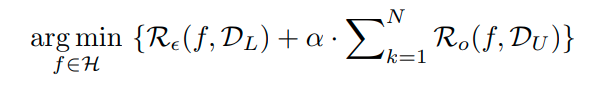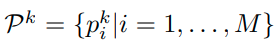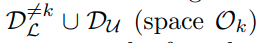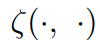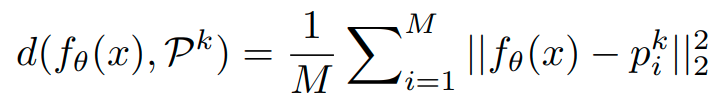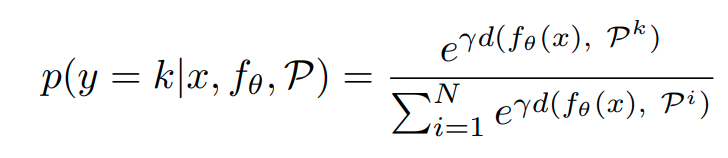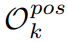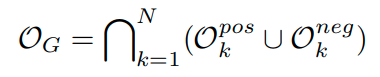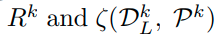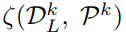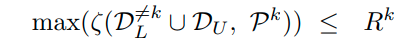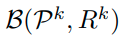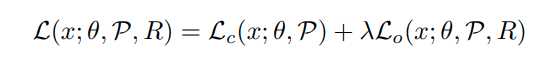Paper
https://arxiv.org/abs/2103.00953
Adversarial Reciprocal Points Learning for Open Set Recognition
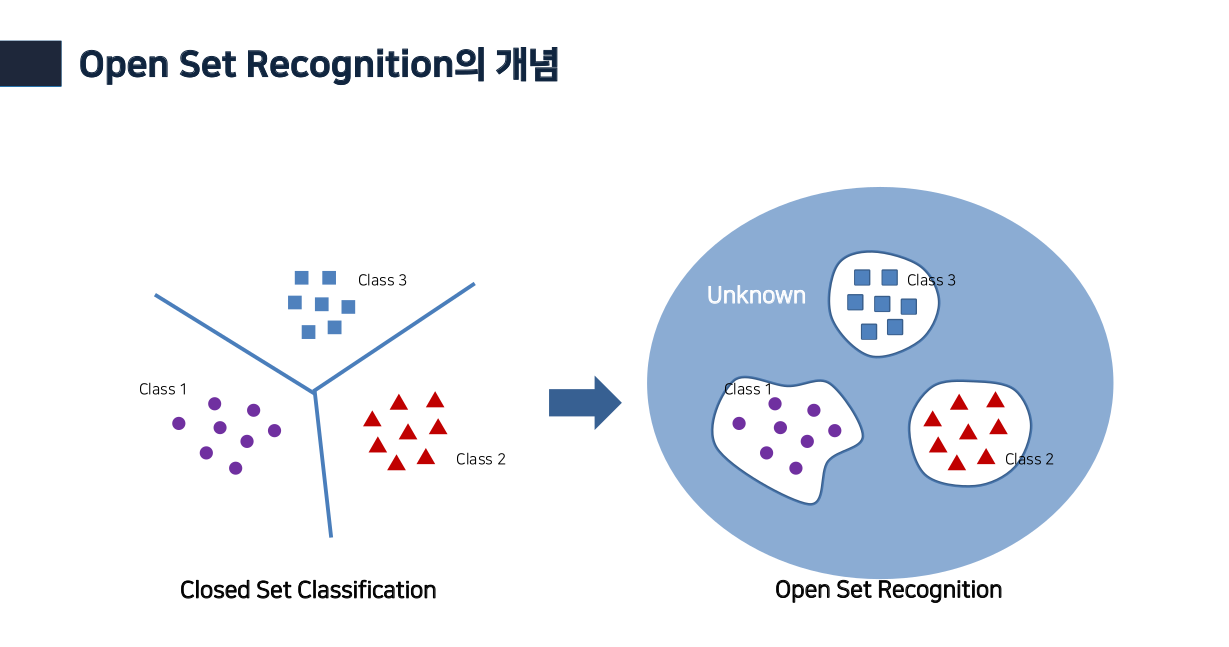
Open set recognition (OSR), aiming to simultaneously classify the seen classes and identify the unseen classes as 'unknown', is essential for reliable machine learning.The key challenge of OSR is how to reduce the empirical classification risk on the label
arxiv.org
Code
https://github.com/iCGY96/ARPL
GitHub - iCGY96/ARPL: Official PyTorch implementation of "Adversarial Reciprocal Points Learning for Open Set Recognition"
Official PyTorch implementation of "Adversarial Reciprocal Points Learning for Open Set Recognition" - GitHub - iCGY96/ARPL: Official PyTorch implementation of "Adversarial Reciproc...
github.com
Introduction
기존의 softmax방법이나 Prototype learning 모두 known data에 대해서만 objective function을 적용해주기 때문에 known class와 unknown class sample이 유사한 곳에 embedding되는 현상을 막을 수 없었다.

기존의 방법들이 known class의 구분을 신경썼다. 따라서 각 known class에 대한 prototype을 지정하거나 신경을 썼다.
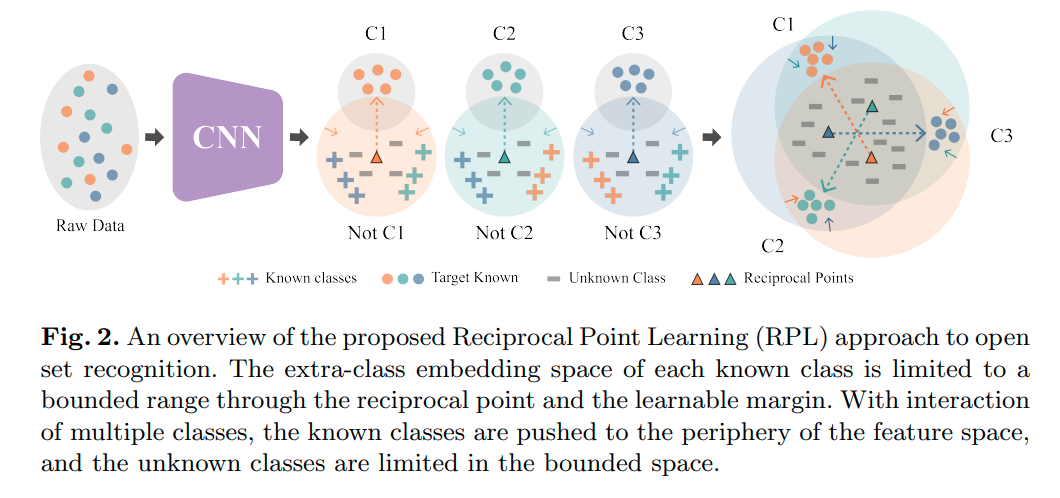
그러나 ARPL의 경우 '반대로 각 Class에 해당하지 않는 것에 대한 center, prototype 지점을 정의'한다. 그리고 그 점을 Reciprocal point라고 명명한다.


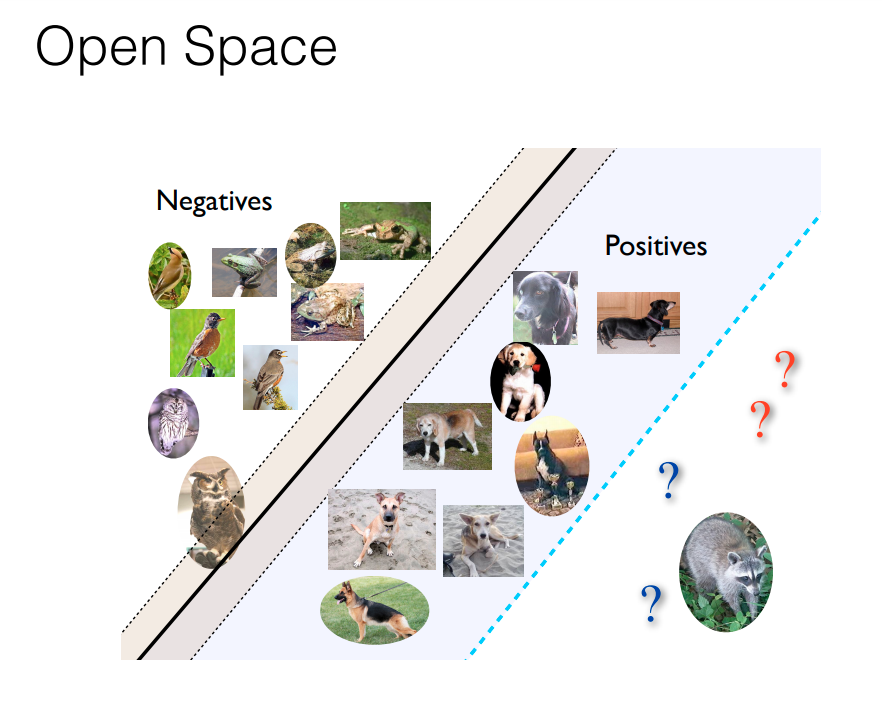
위의 그림 (a)와 같이 특정 클래스가 아닌 sample들의 prototype point를 각 Class에 대해서 지정해준다. (Not C1 , Not C2 , Not C3) 이렇게 하기 위해서는 기존 Class와 reciprocal point의 거리를 멀게 objective를 설정하면 되긴 하지만, unknown sample들이 embedding 되는 위치가 적절히 bounded되지 않는다는 단점이 있다. 때문에 논문에서는 open space를 최대한 줄이기 위한 bound를 설정해주게 된다.
또한 추가적으로 gan model을 이용해 sample을 생성하고 이를 활용한다. 기존 gan과 다른점은 생성한 sample이 classifier를 통과했을때, recipocal point와 가깝게 mapping이 되도록 유도한다는 점이다. (실제 sample이 아니므로)
이와 같은 유도를 표현한 것이 바로 Fig3.(c)이다.
Method
method를 설명하기 위해 여러가지 용어정의가 필요하다.
Sk 는 k번째 class가 embedding 되는 space를 의미한다. 그러므로 k번째 class에 대한 open space는 다음과 같이 정의된다.

그리고 k class에 대한 open space Ok는 다음과 같이 나눌 수 있다.
k class가 아닌 다른 known class들이 mapping되는 O pos k , 그리고 나머지 unknown class가 mapping 되는 O neg k,
그러므로 다음과 같이 표현이 가능하다.
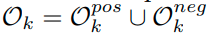
이렇게 정의하였을 때, 다음과 같은 에러를 줄이는 것이 objective이다.
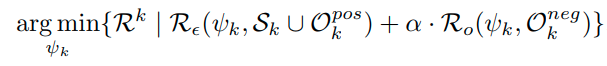
첫번째 term은 classification loss term이고, 두번째 term은 open space를 줄이는 term이다.
open space, R_0는 다음과 같이 정의된다.
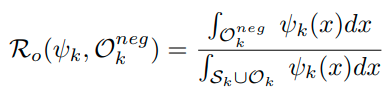
식을 해석하면, 아래는 전체 embedding space를 의미하고, 위는 unknown class sample이 embedding되는 space를 의미한다. 즉, 전체 embedding space중에서 unknown class sample이 embedding되는 space의 비율을 open space라고 정의한다. 그리고 본 논문에서는 이러한 space를 줄이는 것을 목표로 한다.
이러한 loss term을 각 Class 모두에서 행하기 때문에 아래와 같이 표현이 가능하다.
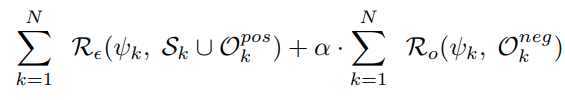
이를 다시 표현하면 아래와 같다. ( one vs rest를 multiclass classification 형태로 변형)
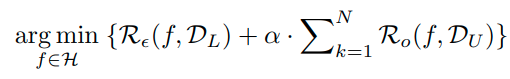
이때, D_L은 labelled data이고, D_U는 unlabelled data이다.
class k의 reciprocal point를 P k라고 나타내면, reciprocal point는 k class에 속하지 않는 sample들의 Prototype을 의미하기 때문에 O_k에 속하는 sample들은 S_k에 속하는 sample보다 P_k에 가까워야 한다.
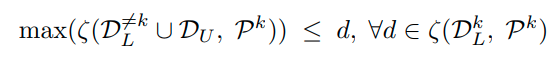
위의 식을 살펴보면, K class에 속하지 않는 labeled data및 unlabeld data들과 reciprocal point Pk과의 거리를 쟀을 때, 가장 큰 값을 추출하더라도, k-class에 해당하는 labeled data sample과 P_k와의 거리보다는 작길 바라는 식이다.
이때, distance는 다음과 같이 정의된다.
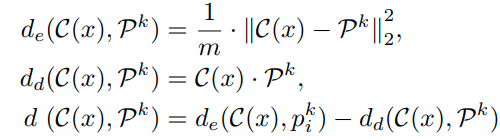
de는 둘간의 euclidean distance를 줄이겠다는 의미이고, dd는 둘간의 각도를 줄이겠다는 의미이다.
각도의 경우 (-)를 붙여서 값이 작을때 , 즉 각이 클때, 거리가 먼것으로 정의하였다.
Classification probability는 아래와 같이 정의한다.
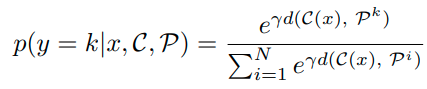
식의 의미는 다음과 같다. 분모는 normalization term이고, 모든 reciprocal point와 sample이 embedding된 위치와의 거리를 구한다. 그리고 분자의 경우 해당 class k에 대한 reciprocal point에 대한 distance이다. reciprocal point와의 거리는 멀수록 해당 class일 확률이 높기 때문에 위와 같이 식을 정의한다.
이에대해서 NLL loss를 적용함으로 classsicfication에 대한 optimization을 수행한다.
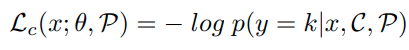
이러한 objective function을 unknown sample과 known sample에 대한 거리를 maximization하기는 하지만, open space O_k에 대해서 제약이 없기 때문에 S_k와 O_k간의 overlap이 발생한다는 단점이 있다.
그 다음 open space risk term을 다루기 위해서 본 논문에서는 Adversarial Margin Constraint (AMC)를 제안한다.
open space는 위에서 말한 것처럼 O pos k , O neg k로 나뉜다. 모든 k class에 대해서 open space를 모두 더하면 다음과 같이 표현이 가능하다.
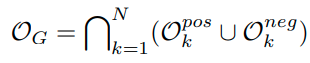
S_k와 O_k를 잘 분리하기 위해서는 O_k의 space를 잘 bounding하는 것이 중요하다.
그래서 다음과 같이 recipocal point와 해당 하는 k 클래스의 'not k class' sample들의 거리를 특정 R값이 이하로 bounding하여 준다.
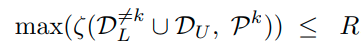
물론 이러한 bounding만으로는 Openspace를 모두 바운딩하는 것은 불가능하다.
아무튼 아래와 같이 tranining sample과 해당 class reciprocal point의 거리를 최소한 R이상을 만들도록 함으로,
간접적으로 open space에 있는 sample들은 reciprocal point와 R이하의 거리를 가지도록 만든다.
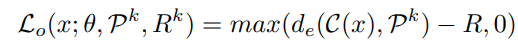
위의 식과 classfication loss를 합치면 아래의 효과를 지닌다고 말하고 있고, 그에 대한 증명을 하고 있다.
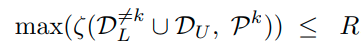

이러한 것을 multi class에 대한 식으로 표현하면 다음과 같다.
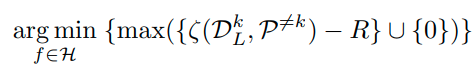
그래서 앞의 내용을 종합하면 아래와 같이 Loss 식을 구성할 수 있다.

자세한 알고리즘은 다음과 같다.

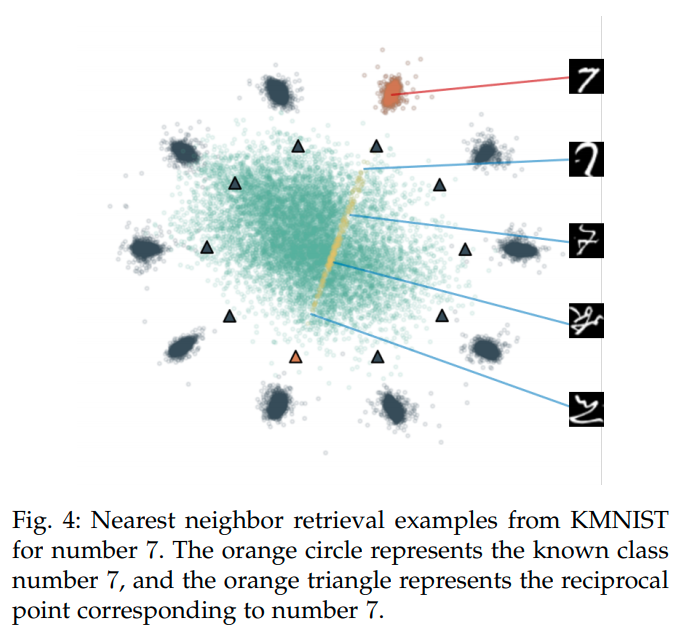
이렇게까지 하면 unknown sample을 어느정도 걸러낼 수 있으나, generator로 부터 생성된 sample까지 cover하지는 못한다. 그러므로 Confusing samples (CS)를 생성해서 이용함으로서 unknown class sample을 더 잘 걸러내도록 한다.

일단 생성하는 sample은 gan을 이용한다.
gan에 대한 수식은 일단 일반적인 gan과 동일하다.
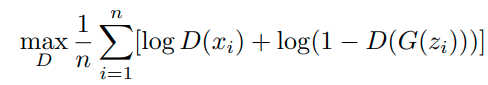
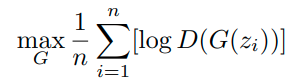
여기다가 optimization 식을 하나 더 추가해준다.
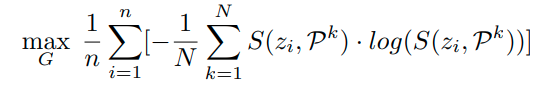
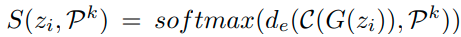
위 식은 기존의 Classsifition의 NLL Loss식과 동일하나 Minimization이 아니라 Maximization하는 것이 다르다.
위 optimization 식이 만족하는 경우는 confusing sample이 reciprocal point에 가깝게 embedding되는 경우이다.
논문에는 아래와 같이 표현되어 있다.

따라서 GAN 네트워크에 대한 Optimization식을 표현하면 다음과 같다.
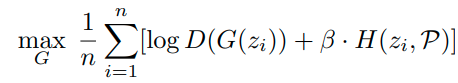
이렇게 생성하는 경우, 결과론적으로 Confidence Calibrated 논문에서 uniform에 fitting해서 sample을 generating하는 것과 같은 효과를 가지게 된다. (realistic하지만, unknownc class의 경계에 위치하는 sample)

또한 생성한 sample을 이용해서 추가적으로 Enhancement하는 term을 추가해준다.
생성한 sample의 경우, uniform distribution에 다시 fitting 해준다. ( Classificaition 부분에서 enhancement해줌.)
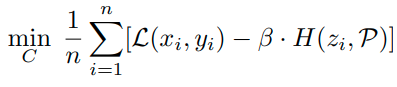
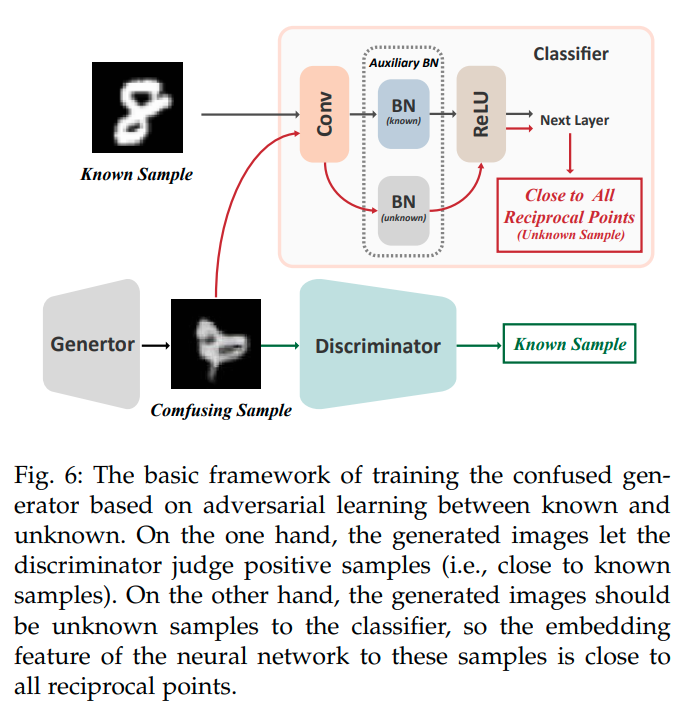
또한 real sample과 생성된 sample들이 같은 domain에 위치하는 것을 막기 위해 Auxiliary Batch Normalization(ABN)을 추가한다. 방법은 real sample과 generated된 sample들에 대해서 batch normalization을 따로 해주는 것으로, 실제로 성능향상에 효과를 보았다고 한다.

Experiments
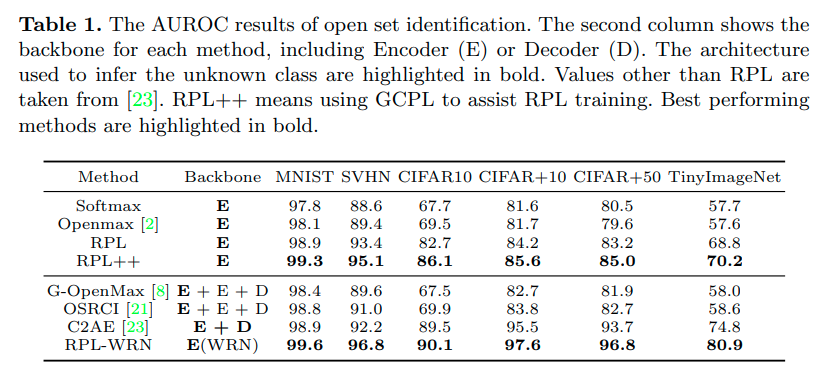
먼저 network는 OSRCI network와 동일하다. gan model은 confidence calibrated classifier와 동일한 model을 사용하였다.
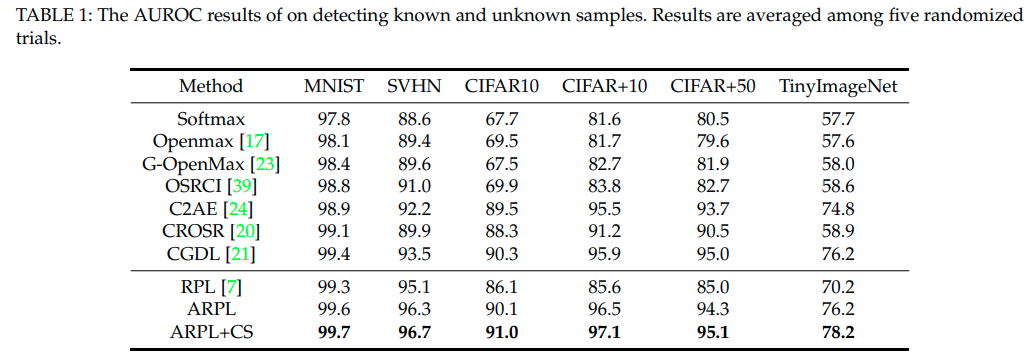
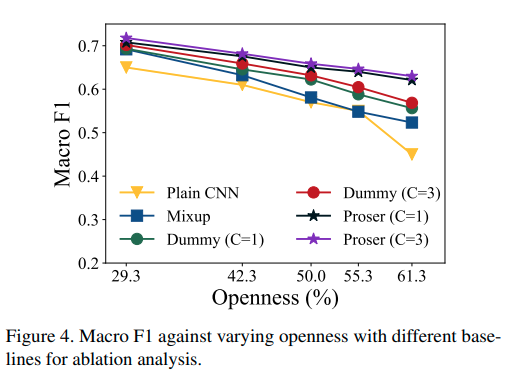
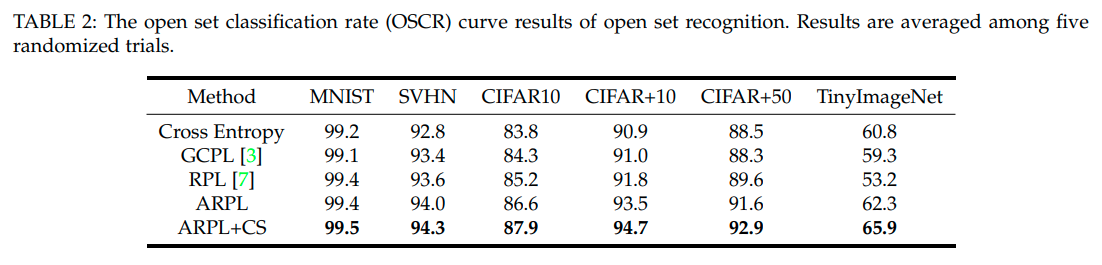
본 논문에서는 OSCR이라는 척도로도 성능을 비교했는데, Classification을 잘 맞춘 비율과 Openset을 잘맞추는 비율을 threshold값을 변화해가며 그린 curve라고 보면 된다. (기존 AUROC는 classification 성능이 높을 필요는 없었음)
-OOD evaluation
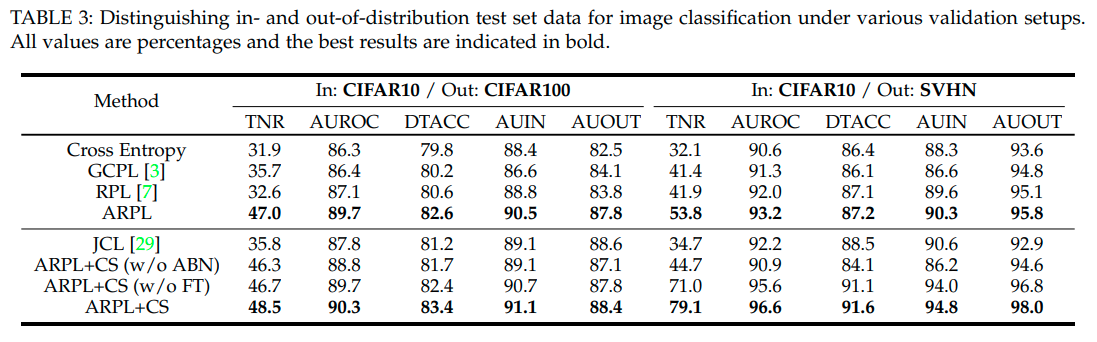
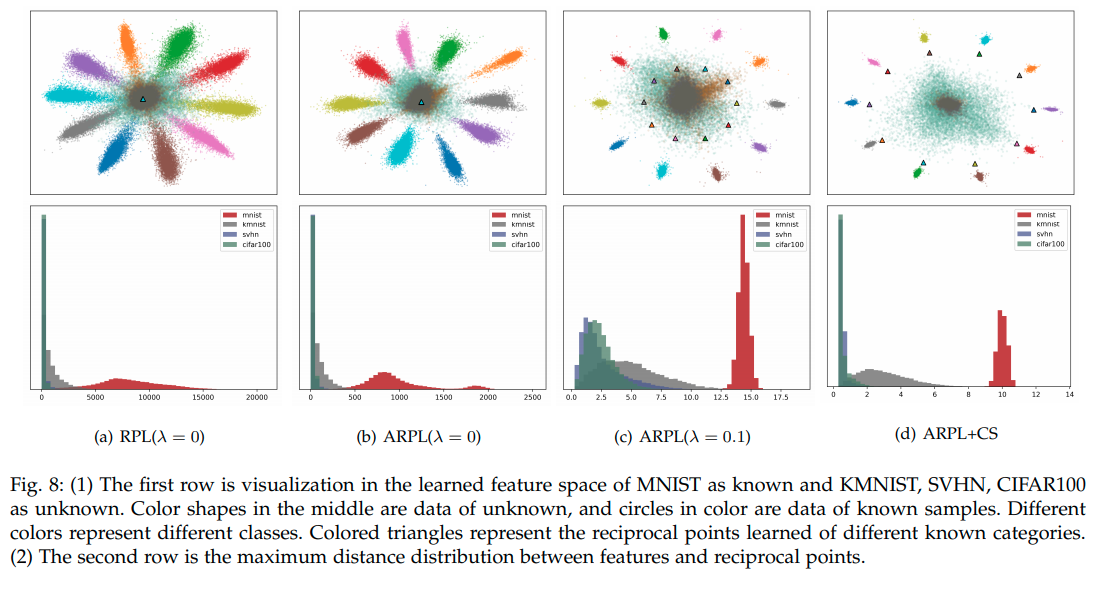

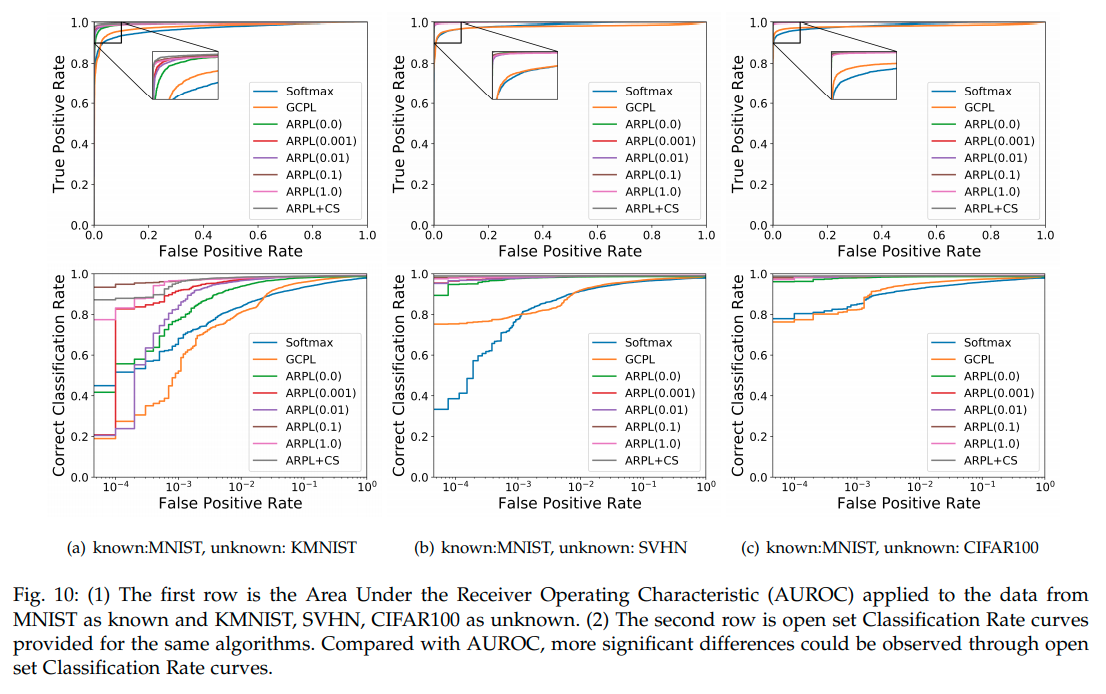
Summary
본 논문은 기존의 method들이 각 class에 대해서 prototype을 설정하고 이에 맞춰서 학습을 진행한것과 달리,
각 Class가 아닌 sample에 대해서 prototype을 설정하고 reciprocal point를 설정한 것이 특징이다.
이를 위해서 각 trainining class k에 대해 reciprocal point와의 거리가 멀어지도록, 학습을 진행한다. 또한 reciprocal point와 training sample간의 거리가 최소한 R보다는 크도록 만든다.
이렇게 학습하는 것이 원래 목적인 unknown class sample이 reciprocal point에 R이하로 bounding되어 embedding되는 효과를 지닌다고 논증하고 있다.
또한 이것에 추가하여 Confusion sample(CS)을 생성하고, 이를 추가로 학습에 이용한다.
이때, confusion sample은 Confident-Calibrated 논문에서 sample을 생성하는 것처럼, trainining sample과 유사하지만 unknown class sample을 생성한다. (자세한건 위 수식 참고) 또한 생성한 sample을 다시 uniform distribution에 mapping한다.
그리고 ABN이라는 생성한 sample에 대해서만 따로 Batch normalization을 적용하여 생성한 sample과 기존의 real sample 과의 distribution이 겹치지 않도록 한다.
Pros
내가 생각하는 좋은 점은 open space를 bounding 시킨 점인듯하다. reciprocal point라는 개념도 좀 재밌긴 하다.
ABN 모듈도 작긴 하지만 신선한 생각이라고 느껴졌다.
Cons
split을 기존 논문들과 다른 split을 사용했다. 결국 좀 정당한 evalution이 이루어지지는 않은 논문이라고 생각한다.
그리고 샘플이 generation하여 추가로 학습하는 부분은 confident-calibration 논문과 너무 유사하다.
단지 자신의 method에 적용할 수 있도록 수정한 것 밖에 없다고 생각한다.
'Paper > Openset recogniton' 카테고리의 다른 글
| Counterfactual Zero-Shot and Open-Set Visual Recognition: CVPR 2021 (0) | 2021.07.14 |
|---|---|
| Open Set Learning with Counterfactual Images : ECCV 2018 (0) | 2021.07.07 |
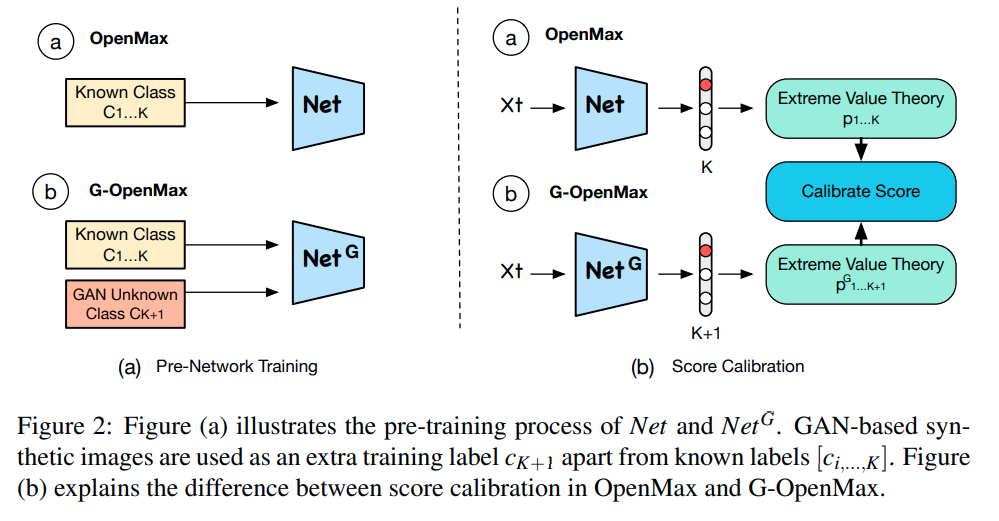
| Generative OpenMax for Multi-Class Open Set Classification : BMVC 2017 (0) | 2021.06.29 |
| Toward Open Set Deep Networks : CVPR 2016 (0) | 2021.06.28 |
| Learning Placeholders for Open-Set Recognition: CVPR 2021 Oral (0) | 2021.05.21 |