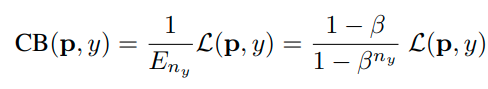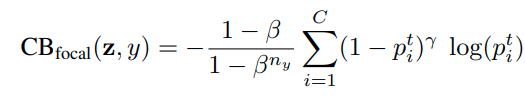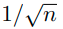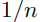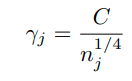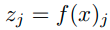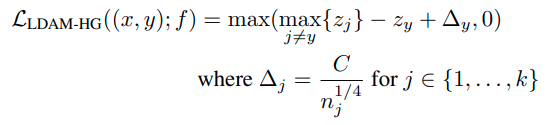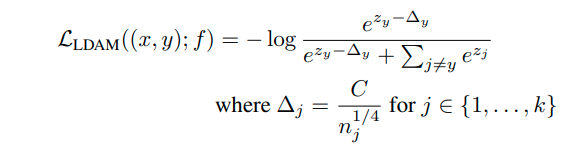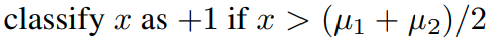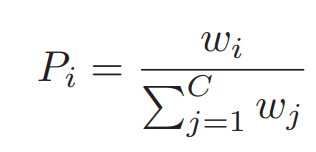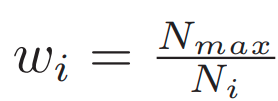Learning to Learn

Paper

arxiv.org/abs/1910.09217

Code

github.com/facebookresearch/classifier-balancing

Abstract

다음과 같은 2가지 현상을 발견하였다.

1) data imbalanced learning은 high-quality representation learning 문제가 아닐 수 있다.

2) 가장 단순한 instance-balanced sampling을 통한 representation learning과 더불어 classifier만 adjusting하는 것이 가장 좋은 성능을 보일 수 있다.

Introduction

기존의 방법들은 representation과 classifirer를 따로 분리하지 않고 joint learning을 수행하였다. 

그러나 이러한 방법들은 imbalanced learning에 대한 성능 향상이 어디서 오는 것인지 알 수 없다는 단점이 있다.

그래서 본 논문에서는 representation learning과 classifirer learning을 decoupled해서 분석한다.

representation learning을 비교하기 위해 다음과 같이 3가지 방법을 사용하고 비교해본다.

1) instance-based sampling

2) class-balanced sampling

3) mixture of them

classifier learning을 비교하기 위해 다음과 같이 3가지 방법을 사용하고 비교해본다.

1) re-training the parametric linear classifier in class-balancing manner

2) non-parametric nearest class mean classifier: which classifies the data based on their closest class-specific mean representations from the training set

3) normalizing the classifier weights, which adjusts the weight magnitude directly to be more balanced, adding a temperature to modulate the normalization procedure.

Method

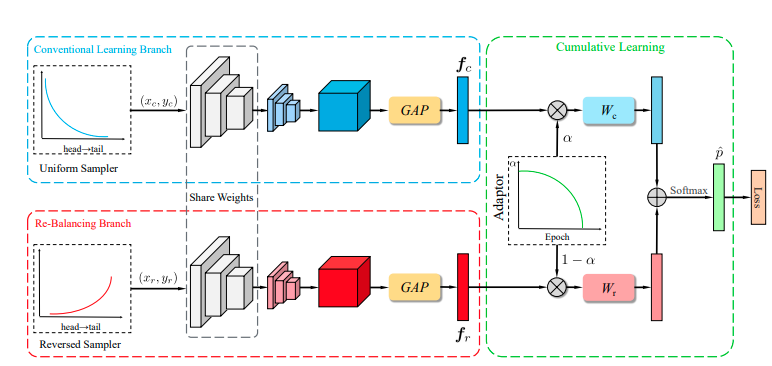
- Sampling strategies

Sampling은 아래와 같이 class당 sampling될 확률을 정의함으로서, 수행되어진다.

이때, q는 sampling 전략을 나타내는 변수이며, 1, 0, 1/2 중 하나의 값을 가진다.

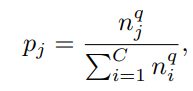
1) Instance-balanced sampling

q=1 일때 instance-balanced sampling을 수행하게 된다. class당 가지고 있는 sample의 수에 비례하여 

sampling을 수행하게 된다.

2) Class-balanced sampling 

q=0 일때, 이며, class당 sampling하는 확률을 모두 동일하게 가져가는 전략이다.

3) Square root sampling

q=1/2이며, sample의 수의 squre root에 비례하여 sampling하는 기법이다. 

4) progressively-balanced sampling

본 방법은 Instance-balanced sampling과 Class-balanced sampling을 혼합한 방법이다.

초반 epoch에는 instance-balanced 기반으로 sampling을 진행하다가 일정 epoch이후에는 class-balanced 형태로

변형되는 sampling기법이다. 자세한 수식은 위와 같다.

- Loss re-weighting strategies

focal-loss, LDAM loss가 대표적으로 있다.

Classification for long-tailed recognition

1) Classifier Re-training (cRT)

representation learning 부분을 fixed하고 classifier만 class balanced 형식으로 다시 학습시키는 방법을 말한다.

2) Nearest Class Mean classifier (NCM)

먼저 각 train data의 class의 mean feature representation을 구한 다음, 이후 query vector의 L2 normalized feature를 활용해서 cosine similarity나 Euclidean distance를 이용해서 nearest neighbor search를 수행한다.

3) τ-normalized classifier 

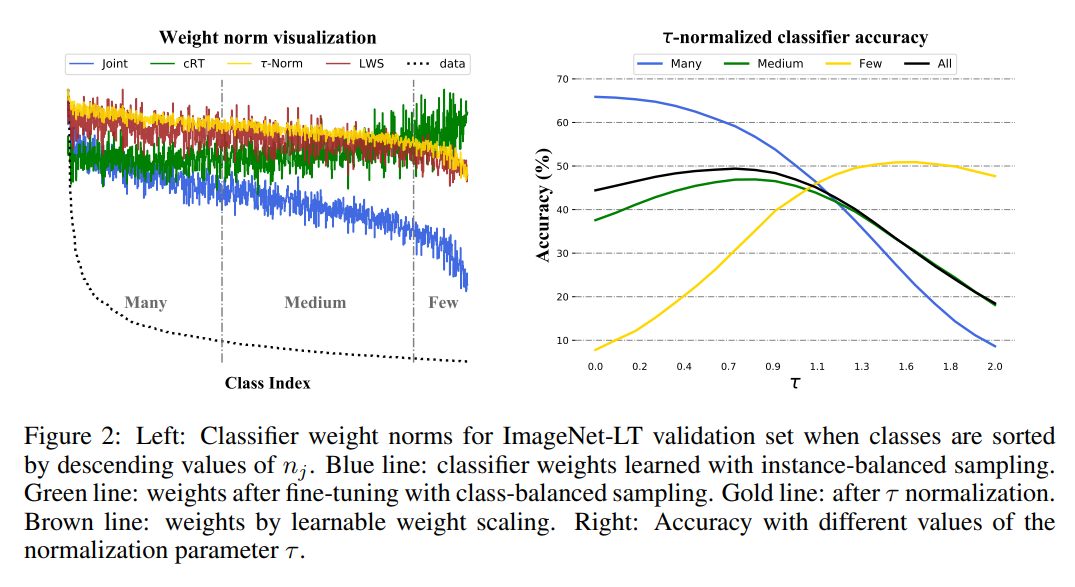
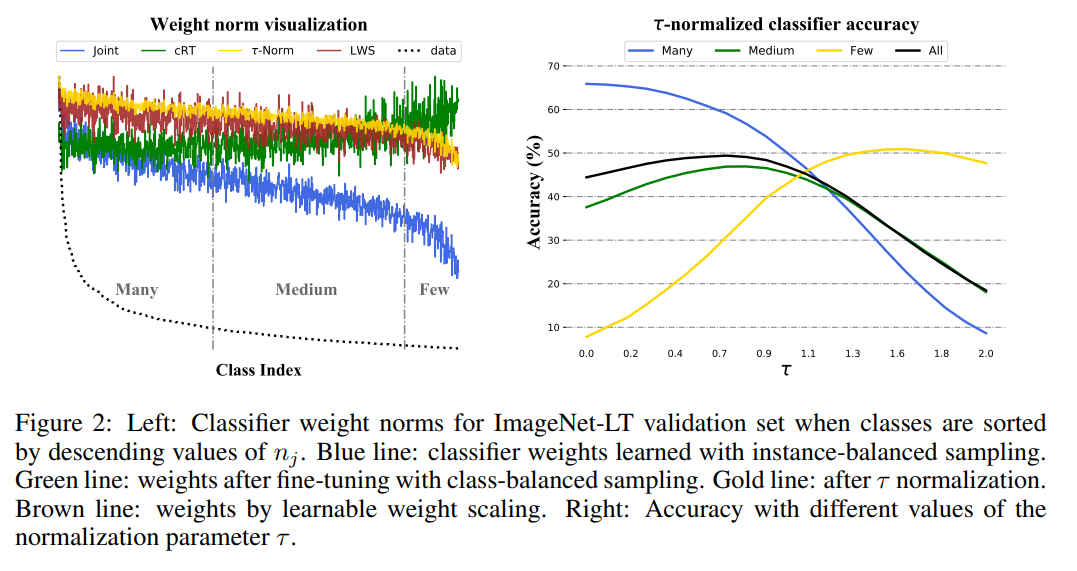
-instance-balanced sampling의 경우, weight값이 class sample 수에 비례하는 것을 확인할 수 있다.

(sample수가 많은 class의 경우 더 넓은 boundary를 가지게 되고, 이것이 weight값의 크기로 나타남)

-class-balanced sampline의 경우, class마다 sample수가 동일하기 때문에 weight의 값이 class마다 비슷하게 형성되는 것을 확인할 수 있다. (decision boundary가 유사해짐.)

- τ-normalization은 이 2가지 방법의 중간 정도의 방법이다. instance-balanced sampling의 weight에다가 normalization을 하여 'smoothing'한다.

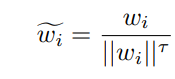
이때 τ는 0~1 사이에서 결정된다.

- Learnable weight scaling (LWS)

scaling하는 정도는 학습을 통해서 얻는 방법을 의미.

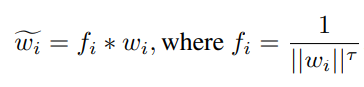
Experiment

-Sampling strategies and decoupled learning

- joint training scheme

classifier와 representation learning이 함께 이루어지는 방식이다. 90 epoch 동안 cross-entropy loss 및 instance-balanced, Class-balanced, Square-root, Progressively-balanced.  

- decoupled learning schemes

 classifier만 다시 training 한다. cRT , NCM, τ-normalized classifier가 사용된다. 

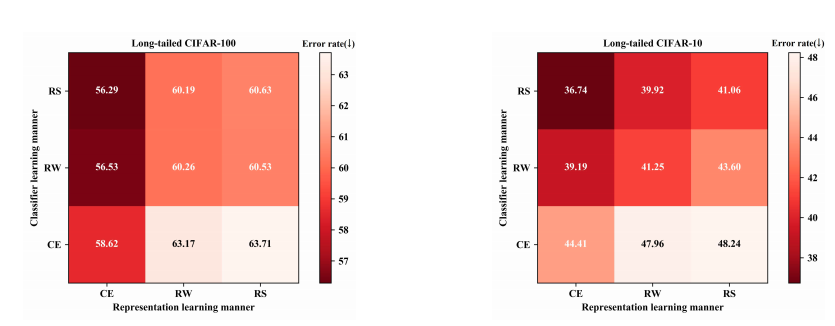
먼저 joint의 경우 더 나은 balanced 방법을 적용할 수록 성능이 향상되는 것을 확인할 수 있다.

(joint 부분만 보면서 세로로 분석하면 됨)

decoupled learning을 하는 경우, non-parametric 방법인 NCM을 적용한 경우라도 오히려 성능이 크게 향상되는 것을 볼 수 있다. parametric한 방법은 더욱 성능이 향상 된다. (가로축으로 성능 변화 살펴보면 됨)

여기서 중요한 발견 중 하나는 representation learning에 있어서 instance smapling이 가장 성능이 높다는 것이다.

이는 data-imbalanced issue는 high-quality representation을 배우는데 상관이 없음을 알려준다. 

위 그림은 각 방법에 대한 decision boundary 형성을 그림으로 나타낸 것이다. 

τ 가 0 인 경우는 normalization을 전혀하지 않은 경우이고,  sample수에 비례해서 decision boundary도 정해지기 때문에 더 많은 sample을 가진 class가 더 넓은 decision boundary를 지님을 알 수 있다. τ가 1인 경우에는 normalization이 적용되기 때문에 좀 더 balanced된 boundary가 형성된다. Cosine 같은 경우 모두 같은 크기의 boundary가 형성된다. 마지막은 각 class마다 mean을 구하고 L2로 nearest neighbor 형태로 classifying을 할때, 나타나는 decision boundary를 나타낸 것이다.

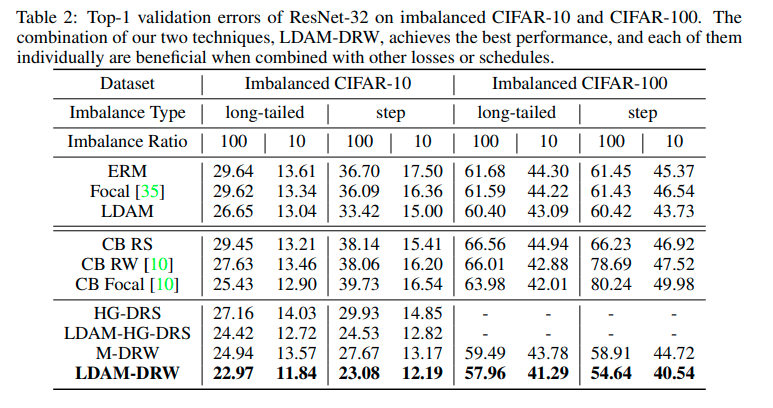
results

Paper

openaccess.thecvf.com/content_cvpr_2016/papers/Huang_Learning_Deep_Representation_CVPR_2016_paper.pdf

Method

imbalanced problem의 근본적인 문제점은 minority class를 학습하기 위한 sample이 부족하다는 것인데, minority class에 대해서 4개의 anchor를 설정함으로 majority class에 비해 더 많은 학습 및 embedding을 형성하도록 하는 방법이다.

먼저 embedding 공간을 L2-norm이 1로 제한된 공간에 놔둔다.

- Quintuplet Sampling

quintuplet은 다음과 같이 정의된다. (그림 참고)

이를 통해 다음과 같이 거리를 설정한다. (위 그림 참고)

이러한 quintuplet method는 2가지 메리트가 있다.

1) Triplet loss는 단순히 같은 class끼리는 당기고 다른 class는 떨어트리는 방식을 사용한다. 그러나 quintuplet은 class간과 class 내부의 instance level까지 같이 고려하기 때문에 더 rich한 feature를 추출할 수 있다는 장점이 있다. 

2) under sampling 방법과 비교하면 information loss가 없고, over-sampling과 비교하면 주로 사용되는 artifitial noise가 없다는 장점이 있다. 실제 구현에서는 mini-batch에 minority class와 majority class 같은 숫자를 넣고 학습을 시킨다.

실제 구현에서 quintuplet을 선정하기 위해서는 이미 위 그림의 cluster들의 초기 형태가 형성되있어야 한다.

그래서 특정 데이터셋에서 pre-trained된 모델을 사용하여 feature를 추출하고 이를 통해 k-means clustering을 하여 cluster를 형성한다.

이러한 clustering을 좀 더 robust하게 하기 위해 5000 iteration마다 cluster 형성을 새롭게 업데이트 한다.

- Triple-Header Hinge Loss

위의 그림을 loss function형태로 구현 한 것이다. (잘 모르겠으면 margin loss 참고)

이와 같이 loss를 구현하면 실제로는 아래와 같이 embedding space가 구현된다.

learning하는 방식은 다음과 같다.

실제 학습할 때는 look-up table (dictionary 형태로 거리 저장한다는 의미인듯) 그리고 hardest한 학습은 피하기 위해서 실제 training set에서 50%만 random으로 sampling하여 사용한다. 

요약하면 다음과 같다.

- Difference between "Quintuplet" Loss and Triplet Loss

Triplet Loss의 경우 class기반으로 같은 class 끼리는 뭉치게 만들고 다른 class sample끼리는 멀리 떨어지게 만들기 때문에, 실제 imbalanced data의 문제인 적은 sample 수를 가진 class의 적절한 boundary 혹은 margin을 표현하지 못할 수 있다. (실제로는 더 넓은 지역을 cover해야 하지만, few sample로는 넓은 지역을 다 cover 못할 수 있음)

이에 반해 Quintuplet의 경우, class 내부에 또 다른 cluster를 형성하며, 이는 class 내부에서 생기는 variance를 표현할 수 있다. 이를 통해서 좀 더 넓은 class의 margin 및 boundary를 형성할 수 있고. imbalance에서 생기는 적절한 boundary를 형성하는 문제에서 도움이 될 수 있다.

- Nearset Neighbor Imbalanced Classfication 

본 논문에서는 Classification을 위해서 kNN Classification 방법을 사용한다. 

기존 kNN과 차이점은 다음과 같다. 

1) 기존 knn은 sample-wise로 classificaiton을 하였지만, 본 논문에서는 class마다 형성된 cluster-wise로 knn을 수행한다.

2) Classificaiton을 위해 다음과 같은 공식을 함께 이용한다.

요약하자면 assumtion 하는 class에 해당하는 가장 멀리있는 cluster와의 거리와 해당 class를 제외한 나머지 class의 cluster중에서 가장 가까운 거리를 계산해 차이를 구한다. 이때, 위 식의 값이 크다는 말은, 특정 class에 해당하는 cluster와를 max값을 취했는데도 작다. 즉, 가깝다는 의미이고, 특정 class를 제외한 class들과의 거리 중에서 가장 작은 값을 취했는데도 크다. 즉, 다른 class들과는 멀다는 의미이므로, 특정 class에 query가 가장 가깝다고 할 수 있다.

이러한 방식은 다음과 같은 장점이 있다.

1) imbalanced 환경에 더 강건하다:

기존 방법의 경우 가장 가까운 class의 개수를 통해서만 prediction하기 때문에 imbalanced 문제를 해결하기 힘드나 본논문에서 제시한 embedding 방법과 위의 classicification rule을 함께 적용하면, minority class에 대해서도 large margin을 가져갈 수 있기 때문에 강건한 결과를 낳는다.

2) cluster wise search를 수행하기 때문에 속도가 sample-wise에 비해 빠르다.

결론적으로 실제 동작하는 순서는 다음과 같다.

Paper

arxiv.org/abs/2004.00431

Code

github.com/alinlab/M2m

Introduction

Imbalanced data를 다루는 방법에는 여러가지 방법이 있지만 그중에서 re-sampling 방법이 있다.

re-sampling 방법은 minority class의 sample을 생성하여, minority class의 수가 부족한 것을 해결하는 방법이다.

대표적인 re-sampling 방법으로는 SMOTE가 있다.

SMOTE는 minority class의 sampling이 feature space상에 embedding되면 sample들의 linear combination을 하여

새로운 feature space상에 sample들을 생성하는 방법이다.

그러나 minority class의 sample이 아주 작은 경우 sample을 생성하더라도 다양한 sample이 생성되지 않기 때문에,

poor performance를 보여주는 경우가 많다.

Contribution

본 논문에서는 minority sample을 생성하는 새로운 방법을 제시한다. : Major-to-minor Translation (M2m) 

기존 SMOTE 계열 방법들은 minority sample을 추가로 생성하기 위해서 minorrity class의 sample들을 이용했다.

그러나 본 논문에서는 minority sample을 생성하기 위해 majority sample을 이용한다.

M2m: Major-to-minor translation

data imbalanced 문제는 보통 다음과 같이 귀결된다.

일반적인 classification 문제는 train data distribution과 test data distribution이 동일하다고 가정한다.

그러나 imbalnced data 문제는 train data distribution과 test data distribution이 동일하지 않다. 

train data 의 경우 highly imbalanced , test data의 경우 uniform distribution을 가진다.

그래서 imbalanced된 train data를 학습하여, uniform인 test data에 잘 동작하는 것이 목표이다.

M2m method의 경우, 이를 행하기 위해 sythetic sample을 majority class로 부터 생성하여 minority sample에 추가한다. 

이러한 방법에는 image to image translation을 통한 minority image를 생성하는 방법도 존재하겠지만,

추가적인 학습 및 복잡한 방법론이다.

본 논문에서는 majority sample을 target minority sample에 대한 confidence를 maximize하는 형태로 

새롭게 minority sample을 생성한다.

이때 another baseline classifier g를 사용하는데, 이는 기존의 imblanced training data에 대해 standard ERM training을 통해 학습한 classifier이다.

때문에 classifier g는 minority class에 overfitting되어 있으며, balanced test dataset에는 generalize가 잘 되어있지는 않은 classifier이다.

이때 우리는 g를 이용해서 minority sample을 생성할 것이다. 그러므로 g는 majority class의 sample들을 이용해 minority sample들을 잘 생성할 수 있다고 가정한다.

그리고 생성된 sample들을 이용해 classifier f를 balanced testing criterion에 맞추어 새로 학습한다.

이때 g를 이용해 sample을 생성할 때, 사용하는 optimization problem 수식은 다음과 같다.

이때, L은 cross entropy loss이고, λ는 hyper parameter이다.

본 식의 의미는 다음과 같다.

major class의 sample x_0에다가 noise δ를 더해서 minority class sample x를 생성하는데,

이때, g classifier에 input으로 넣어서 target minority class k 에 대한 loss가 최소가 되도록 한다.

그리고 생성된 sample x^*를 f classifier를 학습시키는 데 이용한다. 

이때, 생성된 sample의 경우 f classifier에서 기존 class인 k_0로 분류되지 않도록 regularization term을 넣어준다.

이렇게 하는 경우, x_0에서 생성된 sample x가 f_classifier에서 기존 class인 k_0로 분류되는 것은 막으면서

x_0의 주요한 feature는 남길 수 있다고 저자는 말하고 있다. 

(f_classifier에서도 k_class로 바로 prediction하도록 optimization 수식을 세우면, 주요한 feature가 사라질 가능성 있음)

그림으로 나타내면 아래와 같다.

Underlying intuition on M2m

결론적으로 M2m은 다음 논문에서 제시한 방법을 이용한다.

-> Adversarial examples are not bugs, they are features.

결국 majority class에서 minority class에 대한 non-robust feature을 더하여 sample을 생성하는 형태이다.

Detailed components of M2m

1) Sample rejection criterion

synthetic sample을 생성할 때 중요한 것은, g classifier가 기존 class k_0에 대한 feature는 잘 제거하는 것이다.

그래야 k class의 sample을 제대로 생성했다고 판단할 수 있기 때문이다. 

그러나 g classifier는 완벽하지 않기 때문에, k_0를 이용해 k class의 sample을 완벽하게 생성하지는 못한다.

그러므로 생성된 sample이 오히려 방해가 될 가능성이 있다. 

(k_0에 대한 diciriminative한 feature가 남아있을 가능성이 있음)

이러한 risk는 특히 생성을 위해 사용하는 k_0의 sample수가 작을 경우 더 심해진다. 

이러한 risk를 줄이기 위해서 저자는 synthetic sample을 일정 확률로 rejecting하는 방식을 제안한다.

위 식의 의미는 N_k_0 - N_k의 max 값을 B의 exponential 값으로 이용하겠다는 것이며,

B의 값이 작을수록 classifier g의 reliability가 더 높다는 것을 의미한다.

예를 들어 B=0.999이면, sample을 accepted하는 probability가 N_k_0 - N_k > 4602일때, 99% 이상이다.

B=0.9999이면, N_k_0 - N_k > 4602일때 99% 이상이다. 

이러한 모델링은 effective number 논문에서 참고한것이다.

위 논문에서, larger dataset에서 sample이 하나 추가될 경우 실제로 적용되는 효과는 exponentially하게 decrease된다고 한다.

(그냥 확률적으로 rejection 한다는 것이 불분명함)

만약 synthetic sample이 reject되는 경우, original dataset에 있는  minority sample을 대신 추가해준다.

2) Optimal seed sampling

그 다음 고려해볼만한 사항은 class k_0에 대한 majority seed sample x_0를 어떻게 선정할 것인가에 대한 내용이다.

이를 위해서 저자는 다음과 같은 Q(k_0 | k) 를 design 했다.

이때 2가지를 고려한다.

(a) Q는 acceptance probability P_accept(k0_|k)를 maximize 하도록 정한다.

(b) Q는 가능한 diverse class를 정하도록 한다. 즉 entropy H(Q)를 maximize하도록 한다.

결국 다음과 같이 식을 세울 수 있다.

이 optimization을 최대화하는 Q는 P_accept이다. (why?)

그래서 Q(k_0|k)는 다음과 같다.

위의 Q를 이용해 k_0가 결정되면 x_0는 uniform하게 random sampling 한다.

전 과정을 나타내면 다음과 같다.

Paper

arxiv.org/abs/1901.05555

Code

github.com/vandit15/Class-balanced-loss-pytorch

Introduction

imbalanced-data 문제에서는 re-sampling, re-weighting 방법이 주로 적용된다. 

이러한 방법은 주로 class frequency의 inverse하게 weighting을 적용했었다.

그러나 최근 연구에서 이러한 방법이 poor performance를 보였었고, 

때문에 square root에 inverse 하여 weighting 하는 smoothed version이 제안되었다.

이러한 발견은 다음과 같은 의문을 낳게 되었다.

"다양한 imbalanced data에 따라 어떻게 class balanced weighting을 하는 것이 좋은 것일까?"

위 그림과 같이 highly imbalanced data에 바로 sample 수에 inverse하게 re-weighting 방법을 적용하는 것은 좋은 성능을 내지 못한다. 

일반적으로 생각하기에는 data가 많을 수록 성능이 좋아지는 것이 맞지만, 비슷한 data가 추가되는 경우, 실제로 반영되는 효과는 낮다. 그렇기 때문에 각 class마다 'effective number'를 구하고 effective number를 기준으로 하여 re-weighting을 진행한다.

그래서 이 논문의 main contribution은 다음과 같다.

(1) long-tailed dataset을 다루기위한 effective number of sample의 이론적 분석 및 loss function에 적용하는 class balanced term을 design

(2) class balanced term을 기존의 loss function에 추가함으로써, 높은 성능 향상을 가져옴 (cross entropy, focal loss) 

Effective Number of Samples

1) Data Sampling as Random Covering

먼저 sample들의 effective number를 E_n으로 정의한다. 이때 n은 sampling된 example의 수이다.

수학적으로 너무 복잡해지는 것을 막기 위해 partially overlapped 되는 상황은 제외한다.

기존에 있던 data와 overlapped 되는 확률을 p, overlapped 되지 않는 경우를 1-p로 정의하며,

sampling을 진행할 수록 overlapped 될 확률이 커지기 때문에 p는 커지게 된다.

이때, effective number를 수식으로 나타내면 다음과 같다.

이 수식을 증명하는 과정은 다음과 같다.

먼저 E_1=1이다.  (sample이 단 하나이므로 overlapping이 전혀 이루어지지 않기 때문에 당연한 결과이다.)

그러므로 다음과 같이 수식을 먼저 쓸 수 있다.

그리고 n-1개의 example을 sample하고 n번째 example을 sampling하는 경우를 생각해보자.

n-1개의 sample을 sampling했을 때, expected volume은 E_n-1이 된다. 이때, 새롭게 sample된 데이터가 

overlapped될 확률은 다음과 같다.

그러므로 n번째 example이 sampling되었을 때, expected volume은 

와 같이 된다.

이때, E_n-1을 다음과 같이 가정하면

즉, 처음에 가정했던 식이 맞게 된다. (점화식 형태)

이는 samples의 effective number가 n의 exponential function이라는 것을 알려준다.

B는 0~1사이의 값을 가진다. E_n을 다른 형태로 표현하면 다음과 같다.

이 수식의 의미는 j번째 sample이 effective number에 영향을 주는 정도가 B^(j-1)이라는 것이다.

그래서 all possible data의 total volume은 다음과 같이 계산이 가능하다.

위 식을 토대로 다음과 같은 점근적 성질을 발견할 수 있다.

내용을 해석하면, all possible data N이 커질수록, effectve number of sample의 값은, 실제로 sampling된 숫자 n과 같게 된다.

즉, N이 커질수록 data overlap이 사라지고, 모든 sample이 unique해진다는 것을 의미하며, N=1인 경우는 오직 하나의 prototype만 존재하는 상황을 의미한다.

Class-Balanced Loss

input sample을 x , label을

라고 정의하자. 이때 model이 각 class에 대해 prediction한 probability를 다음과 같이 정의한다.

위의 정의에 따라 loss를 L(p,y) , class i의 number of samples를 n_i라고 하자.

그러면 effective number of samples for class를 다음과 같이 나타낼 수 있다.

이때, N_i 를 특정하게 좋은 값으로 설정하는 건 어려운 일이기 때문에 다음과 같이 dataset에 맞게 설정한다.

class-balanced loss를 적용하기 위해서 weighting vector a를 적용한다. 

이때 weighting은 class i에 대한 effective number of samples에 inverse하게 적용한다.

weighting을 적용했을 loss값의 scale이 달라지기 때문에 아래 식으로 나눠줌으로써, 다시 normalize해준다.

결론적으로 본 논문에서 제시하는 CB (class-balanced) loss는 다음과 같다.

이 loss function을 B를 변화시키며 나타내면 다음과 같다.

B가 1에 가까워질수록 inverse class frequncy에 맞게 re-weighting 된 것을 의미한다.

이러한 class-balanced loss는 모델이나 loss function에 general하게 적용이 가능한 장점이 있다.

본 논문에는 이를 증명하기 위해서 softmax cross-entropy loss, sigmoid cross-entropy loss, focal loss에 적용하였다.

Class-Balanced Softmax Cross-Entropy Loss

Class-Balanced Sigmoid Cross-Entropy Loss

Class-Balanced Focal Loss

Experiments

Imbalance factor는 가장 sample수가 많은 class의 sample 수와 가장 sample수가 작은 class의 sample을 나눈 값이다.

Paper

arxiv.org/abs/1906.07413

Code

github.com/kaidic/LDAM-DRW

Introduction

Imbalanced data 문제는 보통 re-weighting, re-sampling 접근 방법을 많이 사용한다. 이는 train data distribution과 test data distribution을 동일하게 만듬으로써, 문제를 접근한다. 하지만 결국 minority class의 sample의 부족은 overfitting을 발생시킨다는 것은 큰 어려움이다.

그래서 저자는 majority class에 비해 minority class에 강한 regularizing 기법을 적용함으로써, minority class에 대한 정확도를 향상시키는 방법을 제안한다. 

이는 기존의 weight matrix에만 regularization 방법을 적용한 것과 달리, label에도 함께 regularization 방법을 적용한다.

결론적으로 본 논문에서는 label-distribution-aware loss function을 적용함으로써, model의 margin을 minority class에 대해 좀 더 크게 되도록 최적화한다.

Main approach

1) Problem setup and notations

2) Fine-grained generalization error bounds.

일반적인 generalization error bound는 다음과 같다. (training , test data distribution이 동일한 경우)

이는 모델의 복잡도가 증가할수록 overfitiing이 잘되기 때문에, 복잡도에 비례하게 되고, training data 수가 많을수록 

실제 data의 분포에 맞게 학습이 가능하기 때문에 error bound가 작아지게 된다.

그리고 training, test 모두 동일하게 imbalanced distribution인 경우, error bound는 다음과 같이 형성된다.

위의 식의 의미는 class간의 margin중에서도 최소값인 r_min이 크다는 것은 class 간의 boundary가 잘 형성되어있다는 의미이고, error의 최대값이 작아진다는 의미이다.

그러나 위 식에서는 label distribution에 대한 정보는 나타나 있지 않다.(oblivious)

그래서 다음과 같이 fine-grained하여 loss function을 다시 구성한다.

3) Class-distribution-aware margin trade-off

위의 margin 식을 살펴보면 class에 대한 sample의 수가 많을수록 error bound가 작아지는 것을 확인할 수 있다.

즉, minority class에 대한 error bound를 줄이려면 margin값을 크게 해야한다는 사실을 알 수 있다.

그러나 minority class에 대해 margin을 너무 크게 하면, majority class에 margin이 작아지는 단점이 있다.

그렇다면 optimal한 margin은 어떻게 구할 수 있을까?

class가 2개인 binary classfication 문제인 경우 balancd generalization error bound를 다음과 같이 나타낼 수 있다.

( 5번식 참고)

이때, r_1과 r_2는 복잡한 weight matrices이기 때문에 optimal margin을 구하기 어렵다.

하지만 이러한 방식으로 접근이 가능하다. 만약 margin r_1, r_2가 현재 optimal이라면,

shifted bias를 현재 margin에 적용했을때, 아래와 같이 error bound가 더 커져야 한다.

위 식은 다음과 같은 의미를 내포한다.

4) Fast rate vs slow rate, and the implication on the choice of margins.

generalization error bound에는 Fast rate와 slow rate라는 용어가 있다.

의 scale에 따라 bound가 변화하는 경우, 'slow rate'라고 부른다.

위와 같이 변화하는 경우 'fast rate'라고 부른다.

딥뉴럴넷이 충분히 큰 경우 위와 같이 fast rate로 바뀔 수 있다.

Label-Distribution-Aware Margin Loss

위의 binary classificaiton의 경우를 고려하여 저자는 multiple case에 대해서 다음과 같이 가정한다.

그리고 soft margin loss function을 위와 같은 margin을 가지도록 디자인한다. (optimal margin이므로)

(x,y)를 training example이라고 하고, f를 모델이라고 하자. 이때, 

를 model의 j class에 대한 output이라고 정의한다.

이때 hinge loss를 이용해서 

위와 같이 loss function을 구성가능하다.

위 식의 의미는 다음과 같다. label y에 대한 logit과 다른 클래스 logit의 max값의 차이가 최소 △는 되어야 한다.

그러나 hinge loss가 smooth 하지 않은 점은 optimization 과정에서 문제점을 만들어내고, 다음과 같이 cross-entropy loss에 margin을 부여해서 smooth한 hinge loss를 만들어 낼 수 있다.

label y에 대한 logit이 margin보다 커야 loss값을 줄일 수 있음

Deferred Re-balancing Optimization Schedule

re-weighting 방법과 re-sampling 방법은 imblanced dataset을 다루는 주요한 방법이다.

(둘다 uniform한 test distribution에 가깝게 만드는 방법이기 때문)

그러나 re-sampling 방법의 경우 model이 deep neural network인 경우 heavy overfitting이 나타난다고 알려져 있다.

그리고 re-weighting의 경우 optimazation이 불안정하다는 단점이 있다. (특히 extremely imbalanced인 경우)

그래서 이전 연구에서 이러한 optimization 문제를 다루기 위해 복잡한 learninig rate schedule을 적용한 바가 있다.

저자들은 re-weighting , re-sampling 방법 모두다 learning rate를 적절히 annealing 하지 않는 경우, 

ERM보다 오히려 성능이 떨어지는 것을 발견하였다. (all training example에 대해 똑같은 weight를 주는 방법)

annealing을 하기 전에 re-sampling 및 re-weighting 방법으로 생성된 feature의 경우 오히려 안좋은 것으로 확인되었다.

그래서 다음과 같은 defered re-balancing training procedure를 만들었다.

먼저 LDAM loss를 vanila ERM (no weighting) 방법을 사용하여 training 시킨다. 그리고 이후에 smaller learinig rate를 이용해 re-weight LDAM loss를 적용한다. 실험 결과적으로 training의 first stage(no weighting) 는 second stage(weighting)의 좋은 초기화 방법이 된다. 

Experiments

1) Baselines

(1) ERM loss : 모든 example에 대해서 똑같은 weight를 적용한 방법, standard cross-entropy loss를 사용한다.

(2) Re-Weighting(RW) :  class의 sample size에 inverse하게 weighting한다. 

(3) Re-Sampling(RS) : 각 example을 sampling할때, class sample size에 inverse하게 sampling

(4) CB : Class-balanced loss based on effective number of samples 논문 참고

(5) Focal Loss : Focal loss for dense object detection.  논문 참고

(6) SGD schedule : SGD를 learning rate dacay method 방법을 사용한 것. 

2) Our proposed algorithm and variants.

(1) DRW and DRS : 먼저 Algorithm 1에 적힌 것 처럼 standard ERM optimization을 적용하고 그 다음 second stage때 re-weighting 및 re-sampling 방법을 적용하는 것을 말한다.

(2) LDAM : 본 논문에서 제안된 Loss function을 적용한 것.

3) Experimental results on CIFAR

HG-DRS 는 Hinge Loss+DRS

LDAM-HG-DRS는 Hinge Loss에 LDAM margin을 준 것,

M-DRW는 cross-enropy에 uniform margin을 줘서 사용한 것을 말한다.

Hinge Loss의 경우 100 class에서 optimization 이슈가 있어서 10개 클래스에서만 실험하였다.

Conclusion

1) LDAM loss를 통해 최적화 된 class 별 margn을 찾음 (binary를 통한 추론값을  multi class에 적용

2) 학습 초반 부터 re-weighting 및 re-sampling 기법을 적용하면 feature의 학습이 저해되는 부작용이 있는데,

    처음에는 standard training 방법을 사용하고 이후에 re-weighting 및 re-samping을 적용하는 deferring 방법을 사용함.

Paper

arxiv.org/abs/2006.07529

Code

github.com/YyzHarry/imbalanced-semi-self

Introduction

일반적인 supervised learning에서는 data의 label은 무조건 도움이 된다.

unsupervised learning과 비교해보면 그것을 알 것이다.

그러나 imbalanced learning에서는 상황이 달라진다.

majority class에 의해 decision boudary가 강하게 형성되게 되고,

아래와 같이 decision boudary가 형성되는 경향성을 보이게 된다. 

그래서 다음과 같은 의문을 제기 한다.

그래서 본 논문에서는 imblanced learning에서의 label의 positive한 면과 negative한 면을 살펴보고 이를 semi-supervised learning과 self-supervised learning 방식으로 이용하여 sota를 달성했다.

먼저 positive view는 imbalanced label이 유용하다는 것이다. 그래서 extra unlabeled data를 추가적으로 사용하여 psedo-labeling data를 형성하고 이를 통해 semi-supervised 방식으로 추가적인 학습을 진행하면, imblanced data 학습을 통한 성능이 향상된다는 것을 증명하고 있다.

그리고 negative view는 imbalanced label이 항상 유용하지는 않다는 것이다. imbalanced label만을 이용해 학습할 경우 acc의 최대치의 bound가 정해지게 된다.  그러나 label을 따로 지정하지 않는 self-supervised 방식을 적용하면 imbalanced label만을 이용해 학습할 경우 제한되는 acc의 한계를 넘을 수 있다는 것이다. 본 논문에서는 이를 수식 및 실험적으로 증명하고 있다.

Imbalanced Learning with Unlabeled Data 

먼저 Unlabel Data를 추가적으로 학습에 사용할 때, 어떠한 효과가 있는지 알아보기 위해 이론적으로 살펴본다.

먼저 binary classification 문제를 고려한다. data는 2개의 Gausssian의 mixture P_xy 모델을 사용한다. 

label Y는 positive value (+1) , negative value (-1) 2가지를 같은 확률 (0.5)의 확률로 가지게 된다.

그래서 Y=+1 일때, data X의 label이 +1 인 경우는 다음과 같이 normal distribution을 따른다. ( label 1에 대한 u_1 gaussian)

Y= -1 일때, data X의 label이 -1 인 경우는  다음과 같이 normal distribution을 따른다. ( label 2에 대한 u_2 gaussian)

이 경우 optimal bayes's classifier는 

가 된다.

이 경우, 

가 된다.

이러한 상황에서 base classifier f_b를 정의해보자. (which is trained on imbalanced training data)

그리고 extra unlabeled data

가 주어졌다고 생각해보자.

base classifer f_B를 이용해 unlabeled data에 대해서 psuedo-label을 형성한다.

결과적으로 psuedo-label이 +1인 unlabeled-data set을  

psuedo-label이 -1인 unlabeled -dataset을

로 표시한다.

이때, psuedo-label이 +1로 분류된 data가 실제로 label이 +1인 경우 indicator를 사용해 '1'로 표시해준다.

그래서,

이때 

가 되고, 의미는 f_B가 Positive class에 대하여 p의 acc를 가진다는 의미이다.

유사하게

가 되고, 의미는 f_B가 Negative class에 대하여 q의 acc를 가진다는 의미이다.

결과적으로

로 정의가능하다.

이러한 상황에서, extra unlabeled data를 이용해,

를 배우는 것이 목표이다.

저 parameter를 측정하는 방법은 아래와 같이 측정이 가능하다.

이때 다음과 같은 결과를 얻을 수 있다.

이 결과는 다음과 같이 해석할 수 있다.

1) Training data imabalance를 estimation의 정확도에 영향을 준다.

위 수식을 보면 △ 가 estimation에 영향을 주는 것을 확인 할 수 있다. 즉, imbalance 정도가 estimation에 영향을 준다.

2) unlabeled data의 imbalanced 정도는 good estimation을 얻을 확률에 영향을 준다.

이때, unlabeled data가 balanced인 경우 good estimation을 확률이 증가한다.

그러나 unlabeled data가 balanced하지 않더라도 어찌되었든 imbalanced data를 추론하는 것에는 도움이 된다.

Semi-Supervised Imbalanced Learning Framework

이러한 가설을 기반으로 본 논문에서는 "Semi-Supervised Imbalanced Learning Framework"를 제안한다.

먼저 original imbalanced dataset 으로 부터 학습시킨 intermediate classifier 'f' 를 얻는다.

그리고 이 'f'를 이용하여 unlabeled data D_u로 부터 pseudo-label y를 생성한다. 

이를 이용하여 최종 모델 f는 다음과 같은 Loss식을 이용해 얻는다.

여기서 w는 unlabels weight이다. 

이 방식은 다른 어떠한 SSL 방식에도 적용이 가능하기 때문에 더욱 실용적이다.

Experimental Setup

실험은 2가지 dataset에서 진행되었다.

CIFAR-10, SVHN

CIFAR-10의 경우 CIFAR-10에 유사한 Tiny-imagenet class data를 unlabel data로 사용한다.

SVHN의 경우 extra SVHN dataset을 unlabeled dataset으로 사용한다.

Why good?

이건 SSL을 좀 더 이해해야 될듯

Experiment results

A Closer Look at Unlabeled Data under Class Imbalance

이러한 SSL 방식을 통해 unlabel data를 이용하는 방법은 unlabel data와 original data의 distribution match가 잘맞는 것이 중요하다.

- Data relevance가 낮으면 성능에 저해가 된다. 기준은 Relevance ratio 60% 이다.

Imbalanced Learning from Self-Supervision

Imbalaced data의 label은 어찌되었든 bias를 가지고 있기 때문에 classification 성능에 악영향을 끼치게 된다.

따라서 본 논문에서는 label을 따로 지정하지 않는 self-supervision 방식을 도입하여 성능 향상이 가능함을 보여준다.

먼저 이론적으로 self supervision이 도움이 되는 것을 증명하기 위해 다음과 같은 상황을 가정한다.

d-dimension binary classification, data distribution P_xy  mixture Gaussian을 가정한다.

이때, Y=+1은 prob p_+ 를 가지고, Y=-1은 prob p_-를 가진다. (p_- = 1-p_+) 그리고 p_-는 0.5보다 큰 것을 가정한다.

(major class를 negative로 정의하기 때문임)

Y= +1, X는 d-dimensional isotropic Gaussian이라고 정의할 경우, 

이유는 negative sample이 더 큰 variance를 갖기 때문이다. 

(majority class는 sample수가 많고 그 이유 때문에 큰 variance를 갖는다.)

이 상황에서  self-supervision을 적용하기 전과 적용한 후를 비교하기 위해 linear classifier에 self-supervision을 적용하기 전과 후를 비교할 예정이다.

linear classifier를 

여기서 'feature'는 standard training을 통해 배우는 feature이다.

self-supervised learning을 통해 배우는 feature는 다음과 같이 표현한다.

이때 다음과 같은 결과를 도출할 수 있다.

Theorem 2는 standard training으로는 3/4이상의 acc를 가지지 못한다는 것을 이야기 한다. (B가 3일때)

그러나 self-supervision을 통해 Z를 추출하면 더 높은 정확도를 얻을 수 있다.

위의 내용은 다음과 같은 내용을 의미한다.

처음에 imbalanced dataset의 label을 제거한 후, self-supervised 방법을 통해 f_ss 를 만든 후 imblanced learning을 하는 경우 더 좋은 성능을 보이게 된다.

Self-Supervised Imbalanced Learning Framework

SSP 를 적용하는 방식은 다음과 같다. 먼저 self-supervision 방식을 통해 f를 학습시킨 후, standard training 방식을 적용하여 final model을 만든다. 이러한 방식은 어떠한 imbalanced learning method에 적용이 가능하기 때문에 장점이 있다.

Experimental Setup

RotNet이랑 MoCo를 사용함.

학습은 pretrain, standard train 모두 같은 epoch 적용 (CIFAR-LT 200 epoch , ImageNet-LT 90 epoch)

results

Paper

arxiv.org/abs/1912.02413

Code

github.com/Megvii-Nanjing/BBN

Introduction

Imbalanced 문제는 주로 re-balancing 방법을 통해 접근하여 해결해왔다.

re-balancing

1. re-weighting

2. re-sampling

re-weighting 방법은 학습할 때, sample수가 적은 class의 경우 더 큰 weight를 통해 큰 loss값을 주고

sample수가 작은 class의 경우 저 작은 weight를 부여함으로 작은 loss값을 준다.

www.analyticsvidhya.com/blog/2020/10/improve-class-imbalance-class-weights/

resampling 방법은 sample수가 적은 class에 대해서 sample을 추가적으로 생성하는 방법을 택한다.

가장 대표적인 방법이 SMOTE이다. (Synthetic Minority Oversampling TEchnique)

machinelearningmastery.com/smote-oversampling-for-imbalanced-classification/

SMOTE는 먼저 minority class에서 random으로 example을 select하고 그 example에 대해 k개의 nearest neighbor를 찾는다.

이때 새로 만들어지는 synthetic instance는 k nearest neighbor 에서 하나를 설정하고 (b), a와 b featrure를 linear combination하여 만들어낸다. 

하지만 이러한 re-balancing 접근 방법은 deep feature의 학습에서 영향을 받게 되고

결국 데이터 전체적으로 under fitting되는 단점이 존재한다.

본 논문에서는 re balancing 전략이 어떤 식으로 동작하는지를 살펴보고

deep network를 representation learning과 classifier learning 2가지로 나눠서 수행한다.

representation learning은 일단 일반적인 plain training을 의미한다고 보면 된다.

그리고 classifier learning은 representation learning 때 학습한 것을 paramater 고정시키고,

classifier만 'scratch'부터 새로 학습시킨다.

본 실험은 Representation learning과 Classifier learning을 각각 re-sampling방법과 Cross entropy 방법으로 나누어서

학습해본 결과이다. 실험결과 Representation learning은 re-sampling, Classifier learning은 Cross-entropy 방법을 사용하는 것이 좋다는 결과가 나왔다.

그래서 본 논문에서는 BBN 모델을 제안하며 , 이는 Representation learning과 classifirer learning을 따로 수행하는 형태의 learning방법을 의미한다.

이 모델은 2가지의 branch로 이루어져 있다.

1. Conventional learning branch

원래 long-tail distribution pattern을 그대로 학습하는 용도로 사용된다. (typical uniform sampler 사용)

2. Re-balancing branch 

Re-Balancing Sampler는 tail 쪽 data를 좀더 많이 sampling한다.

이때, a는 Adaptor에 의해 생성되고 , universal feature에서 tail data에 대한 feature를 learning하도록 

조절하는 역할을 한다. 

그리고 a는 각 branch의 parameter를 update하는 control하는 용도로도 사용된다. 

그러면 re-balancing 방법은 어떻게 동작하는 것일까?

deep network는 feature extractor part와  classifier part로 나뉜다.

class re-balancing straregies는 train data distribution을 test data distribution\

의 형태로 바꿔주어서 classification 성능을 향상시킬 수는 있다.

그러나 이러한 방식에 대해 본 논문에서는 가설을 하나 제기한다.

이러한 방법은 classifier learning의 성능은 향상시키지만

universal representative ability 에는 성능을 저하시키는 영향을 준다.

위의 그림을 다시 살펴보자.

Representation learning 방법을 하나로 고정시킨채로 살펴보면

Classifier learning을 CE로 하는 것 보다 RW, RS 형태로 하는 것이 더 성능이 좋은 것을 확인할 수 있다.

이는 classifier weight를 조정하는 re-balancing operation이 test distribution에 적합하여 더 좋은 성능을 내는 것이다.

이와 다르게 Classifier learning 방법을 하나로 고정시킨채 살펴보면

Representation learning의 경우 CE로 했을때 가장 좋은 성능을 보임을 알 수 있다.

즉 discriminative한 deep feature을 학습하는 것에는 RW/RS한 방법이 좋지 않음을 확인할 수 있다.

그래서 본 논문에서는 아래와 같은 framework를 만들고 실제로 적용한다. 

logit은 아래와 같이 weighting한다.

이때 a는 다음과 같은 수식으로 정의되며,  T_max는 최대 epoch, T는 현재 epoch으로 정의된다.

uniform sampler

uniform sampler는 data distribution의 형태 그대로 sampling 하기 때문에, 

data가 많은 many class에 대한 학습이 더 많이 진행되게 되고 따라서 feature의 학습 즉,

representation learning이 더욱 잘 되게 된다.

re-balancing branch

이와 다르게 rebalancing branch는 extreme한 imbalance를 해결하기 위한 것으로

tail class에 대한 classification accuracy를 상승시키기 위한 것이다.

Code

실제 코드 구성은 위와 같다. 

uniform sampler로 부터 sampling한 image_a

rebalancing sampler로 부터 sampling한 image_b

두개의 image를 각각 conventional branch와 rebalancing branch에 입력으로 사용하고

feature_a, feature_b를 추출한다.

이를 통해서 논문의 내용대로 a값을 이용해 이를 조합하고,

loss 또한 image 두개의 label을 이용해 조합하여 loss값을 준다. (mix_up 형태)

Inference Phase

Inference 단계에서는 같은 sample이 두개의 branch에 입력으로 들어가게 되며,

a는 0.5를 적용한다. 

Data sampler - detailed with code

Data sample을 위한 각 클래스간의 sampling 확률 도출 방법은 다음과 같다.

(밑의 식은 reversed sampling)

Visualization of classfier weights

classifier의 weight의  l-2 norm의 크기는 classifier의 preference를 의미한다.

(www.microsoft.com/en-us/research/wp-content/uploads/2017/07/one-shot-face.pdf)

그렇기 때문에 class별 weight의 l_2의 분포값이 작을수록 balance에 맞게 학습된 것을 의미한다.

BNN-CB의 경우 conventional branch를 의미하며, original dataset에 대해서 학습된 것처럼,

majority class에 더 높은 preference를 가지는 것을 확인할 수 있다.

BNN-RB의 경우 reblanced branch를 의미하며, rebalanced distribution에 대해서 학습된 것처럼,

minority class에 더 높은 preference를 가지는 것을 확인할 수 있다.

이 2개를 합친 BNN_ALL의 경우 std가 가장 작은 것을 볼 수 있다.

즉 class에 대한 preference가 골고루 퍼져있음을 알 수 있다.

Conclusion

이 논문은 다음과 같은 장점을 노렸다고 생각한다.

original data로 부터 feature learning의 장점을 얻기 위해 

Conventional branch를 통해서 original distribution에 대해 학습을 진행한다.

이를통해서 backbone네트워크는 좀더 좋은 feature를 학습하게 된다.

이전 실험이 먼저 representation learning을 한 이후에 classifier learning를 RW, RS 형태로 진행한 것 처럼

알파(a) 값을 조정하여 처음에는 uniform sampler로 부터 학습을 시작하고, 이로부터 feature가 잘 학습된 backbone 네트워크로부터 RS/RW 효과를 내는 re-balancing branch로 부터 학습을 늘린다. 

mix-up형태를 사용한 이유는 어찌되었든, conventional learning branch는  최종적으로 W_c가 majority class에 preference를 더 가지도록 학습이 된다. 그리고 Re-Balancing Branch는 W_r이 Minority class에 preference를 가지도록 학습이 된다. 그러나 mix-up형태를 취함으로서 이러한 편향을 balance한 형태로 맞추어 줄 수 있다고 생각되어 진다.