SCAN: Learning to Classify Images without Labels : ECCV 2020

Paper

arxiv.org/abs/2005.12320

SCAN: Learning to Classify Images without Labels

 

Code

github.com/wvangansbeke/Unsupervised-Classification

wvangansbeke/Unsupervised-Classification

 

Introduction

 

 

본 논문은 기존 unsupervised clustering 논문들과 다르게 two-step 형태의 approach를 사용했다는 것이 특징이다.

SCAN (Semantic Clustering by Adopting Nearest neighbors)의 과정은 다음과 같다.

 

- 첫번째는 기존의 Deep cluster가 represetation learning을 통한 classifier output을 통한 clustering 때문에 cluster degeneracy를 발생시키는 문제점을 대비해서 nearest neighbors를 이용해 clustering을 진행한다.

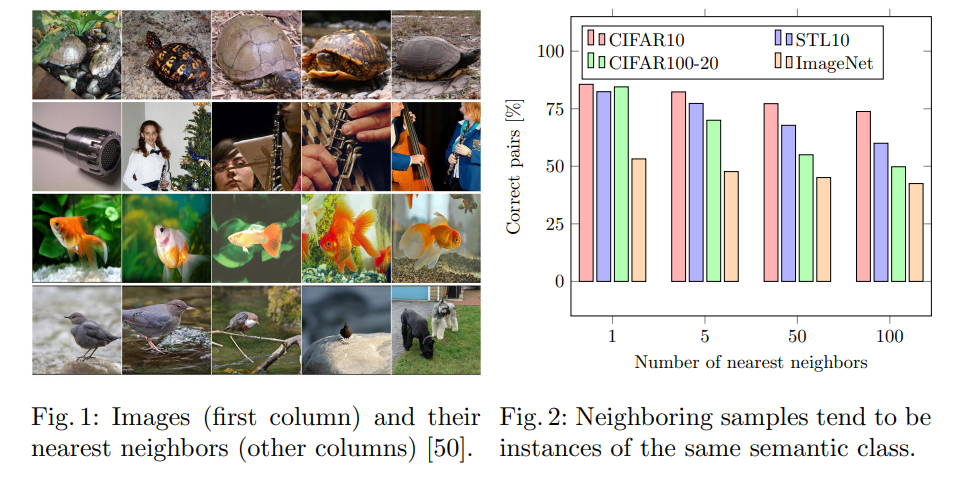
nearest neighbor도 same semantic class에 속하기 때문에 이것이 가능하다. (Fig 2)

 

- 두번째는 nearest neighbor들을 learning의 prior로 활용한다는 점이다. 이는 기존의 방법이 특정 sample과 그 sample에 하나의 augmentation을 적용한 sample을 가깝게 embedding 되도록 학습하는 것에 비해 nearest neighbor들을 가깝게 embedding 시킨다는 차이점이 있다.

 

 

Method

 

- 기존의 방법은 CNN의 prediction을 이용해 k-means clustering을 형성하고, k-means clustering을 통해 형성된 label을 통해 다시 CNN의 학습을 진행하는 것을 반복한다. 그러나 k-means의 초기 label은 네트워크가 학습이 덜 진행된 상태에서 결정되는 부분이기 때문에 high-level information을 추출한 상태가 아니게 되고 최종 목표인 semantic clustering에 오히려 방해가 되게 된다.

 

- 이를 해결하기 위해 representation-learning (self-supervised learning)을 활용한다. 기존의 self-supervised learning의 경우 특정 image에 transformation을 적용하고 각각에 대해 다른 label을 적용하여 다른곳에 embedding 되도록 한다. 그러나 이러한 방식은 유사한 이미지가 비슷한 곳에 위치되어야 하는 semantic clustering에 맞지 않기 때문에 다음과 같이 transformation을 적용한 것과 같은 곳에 위치하도록 loss function을 구성한다. (contrastive learning 참고) 

 

- 이와 같은 방법으로 유사한 class가 가깝게 위치하는 경향을 띄는 것을 실험으로 증명하였다. (Fig 1,2)

 

- 이러한 것이 가능한 이유는 다음과 같다. 첫번째는 모델 Φ_θ가 loss function에 의해서 특정 information을 추출하도록 유도된다. 두번째는 모델 Φ_θ가 추출하는 feature의 크기는 한정되어 있기 때문에 필요없는 information은 버리고, 필요한 high-level information만 추출한다. 

 

- 이러한 motivation으로 먼저 SimCLR이나 Moco와 같은 self-supervised learning을 이용해 feature를 학습하고 이 feature를 이용해 clustering을 진행한다. 그러나 단순히 이러한 방식으로는 cluster degeneracy를 막을 수 없다.

 

-때문에 본 논문에서는 nearest neighbor를 이용한다.

 

-먼저 self-supervised learning을 이용해 feature space를 형성한다. sample X_i에 대해서 K-nearest neighbor를 찾고 이를 N_X_i로 정의한다. 이때, N_X_i가 X_i랑 같은 label로 형성되는 것이 중요한 데, fig 2를 보면 같은 label로 형성되는 비율이 나와 있다. 결과적으로 유의미하게 같은 label로 형성된다고 판단되기에 저자는 k-nearest neighbor를 semantic clustering의 prior로 활용한다.

 

-위의 X_i와 N_X_i를 이용해 classification을 수행하는 새로운 모델 Φ_η을 학습한다. 이때 Φ_η는 맨 마지막단은 softmax function으로 구성되어 있으며,Φ_η(X_i)는 Φ_η 함수의 softmax output을 의미하며, Φ^c_η(X_i)는 X_i가 cluster c에 속하는 확률값만을 따로 추출한 것이다. 

 

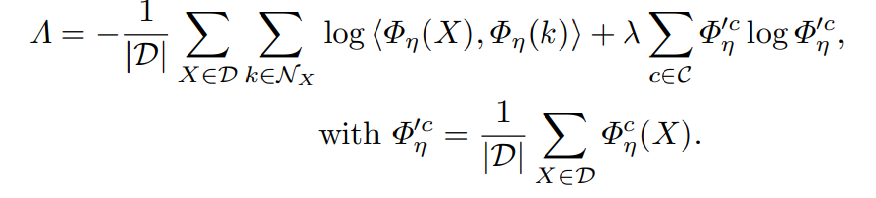
- 첫번째 식은 X의 Φ_η 모델에 대한 softmax output과  X의 nearest neighbor에 대한 softmax output을 dot product한 결과이다. 이때, dot product가 최대가 되는 경우는 두개의 prediction이 one-hot label로 같게 되는 경우이다. 

(그렇게 해서 값이 1이 나오면 log (1)이 되어 loss는 0이 된다.

 

- 그러나 첫번째 식만 있는 경우, 모든 sample을 하나의 cluster로 prediction하는 cluster degeneracy가 발생하게 되고 때문에, 두번째 식 entropy식을 이용해 하나의 cluster로 모두 assign되는 현상을 막는다.

 

- entropy식의 마이너스를 loss function으로 활용함으로 sample들이 다양한 cluster에 assign되도록 만들어준다.

 

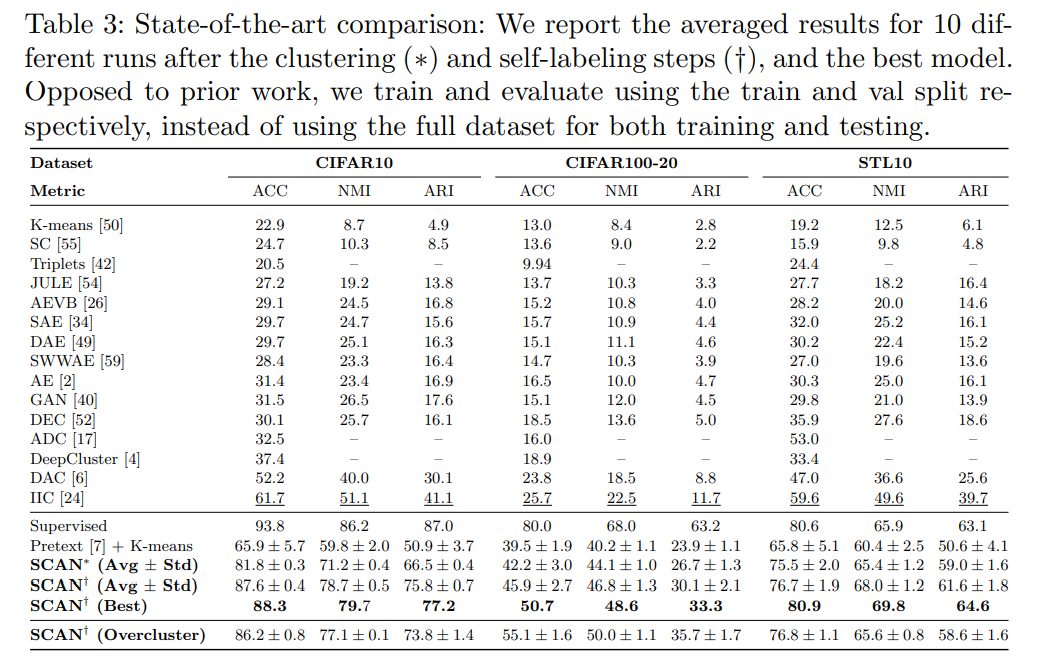
-이때, cluster 수는 실제로는 모르는 것이 맞다. 기존 논문들은 일반적으로 evaluation을 위해 dataset의 실제 label수와 동등하게 cluster수를 설정하여 진행한다. 그러나 꼭 이렇게 설정할 필요는 없고 더 큰 수로 설정해서 각 cluster에 대한 확률이 좀 더 equally하게 나오도록 할 수도 있다. 이에 대한 실험은 Section 3.4에서 진행하였다.

 

- K-nearest neighbor의 K=0인 경우, nearest neighbor를 학습에 사용하지 않겠다는 의미이고, 기존의 논문들 처럼 image sample 하나만을 이용해 augmentation을 적용하고 이들끼리 가깝게 embedding되도록 네트워크를 학습시킨다.

본 논문에서는 K를 늘려가면서 실험을 진행했으며, K가 증가할수록 성능도 함께 증가했음을 보였다.

 

- mutual information을 이용해 optimization을 진행한 'Invariant'(badlec.tistory.com/202) 논문과 비교했을때는 좀 더 직접적으로 sample x와 augmentation한 sample x'을 가깝게 embedding 시키도록 하였다는 차이점이 있다.

 

-추가적으로 본 논문에서는 self-labeling fine-tuning을 통해 noisy nearest label로 인해 생기는 optimization 문제를 correcting하는 과정을 거친다. 

 

-본 논문에서 실험한 결과 sample을 classification network에 통과시켰을때, confidence가 높게 나오는 sample은 제대로 된 cluster에 잘 clustering이 됨을 확인하였다. 따라서 confidence에 대한 threshold를 지정하고 특정 threshold를 넘는 sample에 대해서는 classification network를 재학습하는데 이용한다. 

 

-위의 과정을 정리하면 아래와 같다.

 

 

Experiments

* RA - Random Augment