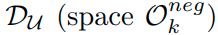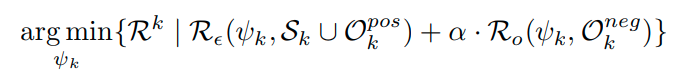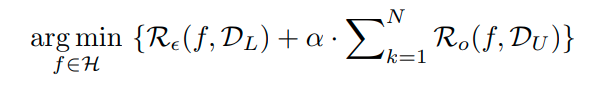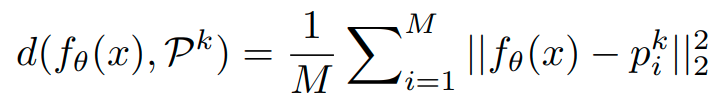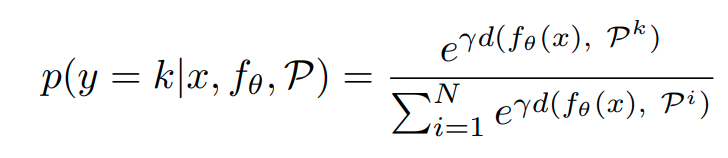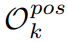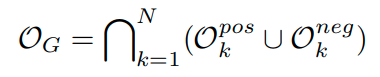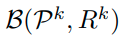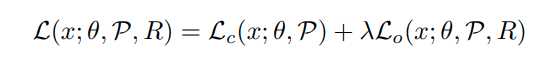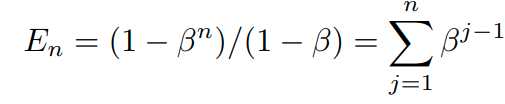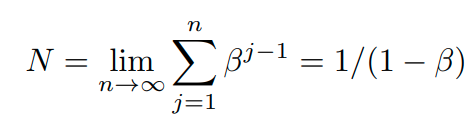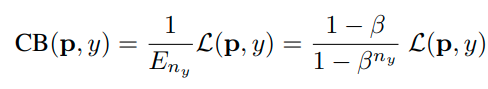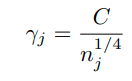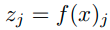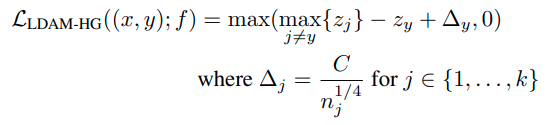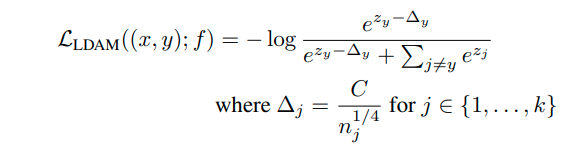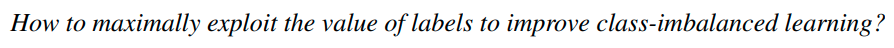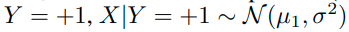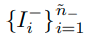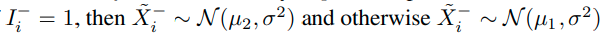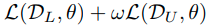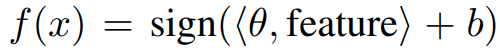Learning to Learn

Paper

arxiv.org/abs/1910.05872

Code

github.com/hankook/SLA

Introduction

그동안의 self-supervised task를 이용한 방법은 multi-task learning의 형태가 많았다.

(Multi task learning은 아래 그림 참고) 

그러나 multi task learning 방식은 단순히 supervised 방식을 사용했을 때 보다 acc gain은 없다. 

그렇다면 어떻게 self-supervision을 fully supervised classfication task에 적용하는 것이 가장 좋은 방법일까? 

Contribution

먼저 multi task learning의 경우 primary network에 대해서 self-supervision task (transformation)에 대해서 invariant하게 만든다. 예를들어 Rotnet의 경우 rotation에 대해 invariant하게 만들어주는 방식이다.

그러나 이러한 invariance는 오히려 task에 대한 난이도 및 복잡도를 증가시킬 수 있다.

예를들어 {6 vs 9} 와 {bird vs bat} 같은 경우 회전때문에 오히여 두 클래스가 더 헷갈릴수도 있기 때문이다.

그리고 이러한 이유 때문에 오히려 multi-task learning이 성능이 더 저하되는 경우가 생긴다.

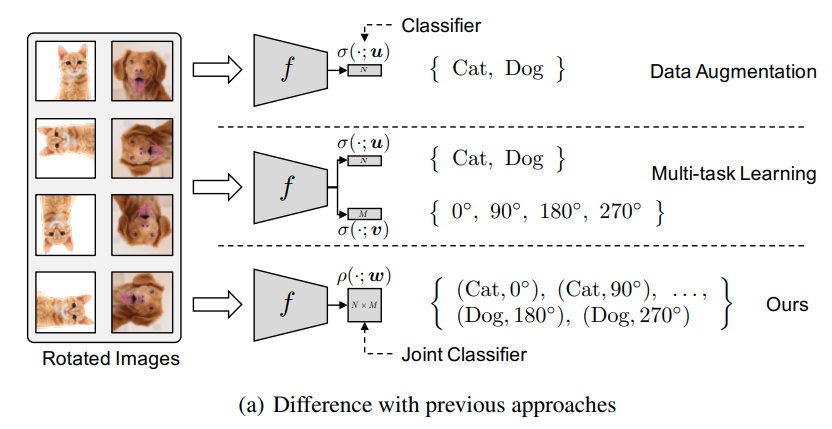
(아래 그림 baseline과 MT(Multi-Task) accuracy 비교)

이러한 문제를 해결하기 위해서, 저자들은 기존의 label과 self-supervision label을 조합한 joint distribution을 제안한다.

예를들어 cifar10 dataset과 Rotnet을 조합하는 경우 10 label * 4label (0, 90, 180, 270) 총 40 label이다. 

이렇게 하면 multi task learning의 경우 class에 대한 label 없이 Rotation에 해당하는 label을 맞추어야 하기 때문에 오히려 classificaition 성능이 떨어지는 상황이 발생하나, joint의 경우 각 input으로 들어오는 image가 어떤 class에 대한 정보를 rotation과 함께 부여하기 때문에 이러한 문제가 해결할 수 있다.

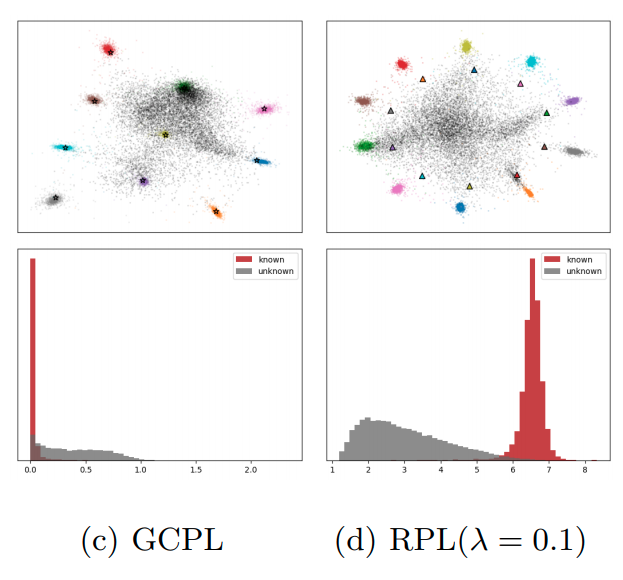
또한 아래 그림과 같이 특정 class에 대한 self-supervision prediction에 대한 결과들을 aggregation하여 앙상블 효과 또한 얻을 수 있다. 

본 논문에서는 self_supervision task로서 Rotation과 Color Permutation 방법을 사용했으며, fully-supervised, few-shot, imbalanced dataset에서 성능향상을 볼 수 있었다.

Self-supervised Label Augmentation

* notation

input :

label : (N은 class의 수)

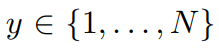
cross entropy loss function:

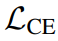
softmax classifier :

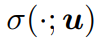
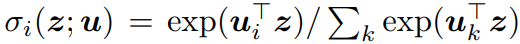
embedding vector of x :

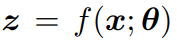
augmented sample using transformation t 

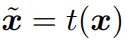
the embedding of the augmetnted sample x:

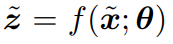
Aggregated inference

label을 joint하여 learning한 이후에 inference의 경우는 다음과 같이 한다.

class에 해당하는 self-supervision transformation의 logit을 모두 더한다.

그렇게 하면 class별 logit이 새롭게 산출되고 이를 softmax를 이용해서 prediction한다.

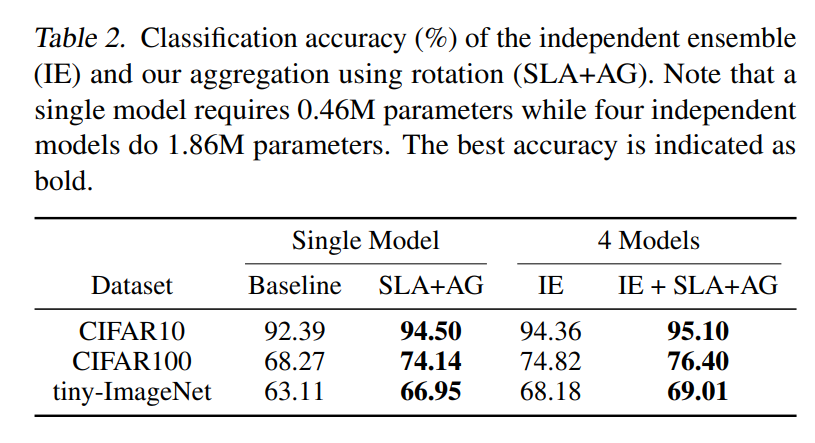
이러한 방식은 앙상블 방식으로 해석할 수 있는데, 

실제로 independent한 여러개의 모델을 앙상블 한 것 보다 더 높은 성능이 나왔다.

Self-distillation from aggregation

aggrregation이 성능향상에 큰 도움을 주기는 하지만, inference과정에서 기존의 label보다 훨씬 많은 label에 대한 

summation 계산과정이 있기 때문에, computation cost가 존재한다. 

이러한 inference과정에서 computational cost를 줄이기 위해서 본 논문에서는 self-distillation방법을 사용한다. 

그래서 aggregated된 knowledge

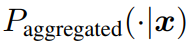
를 다른 classifier에 distillation한다.(그림참고)

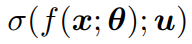
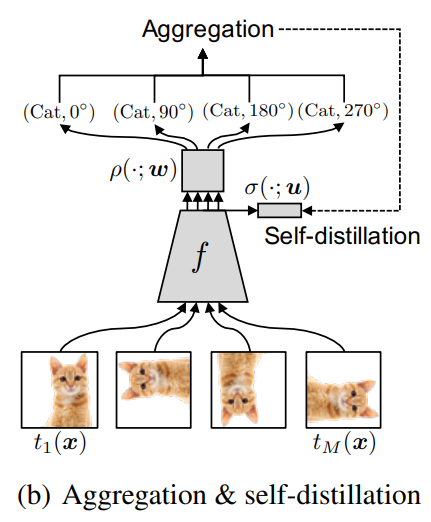
즉 feature extractor에 n*m (label 개수 10*4)의 classifier와 n(label 개수 10) classifier 2개를 놓고, n*m classifier는 label을 통해 학습시키고 n classifier의 경우, distilation을 통해 학습시킨다.

그리고 inference 단계에서는 self-distilation을 통해 학습된 classifier를 이용해 inference한다.

최종적인 loss function은 다음과 같다.

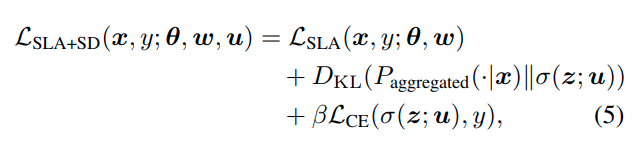
Comparison with DA and MT

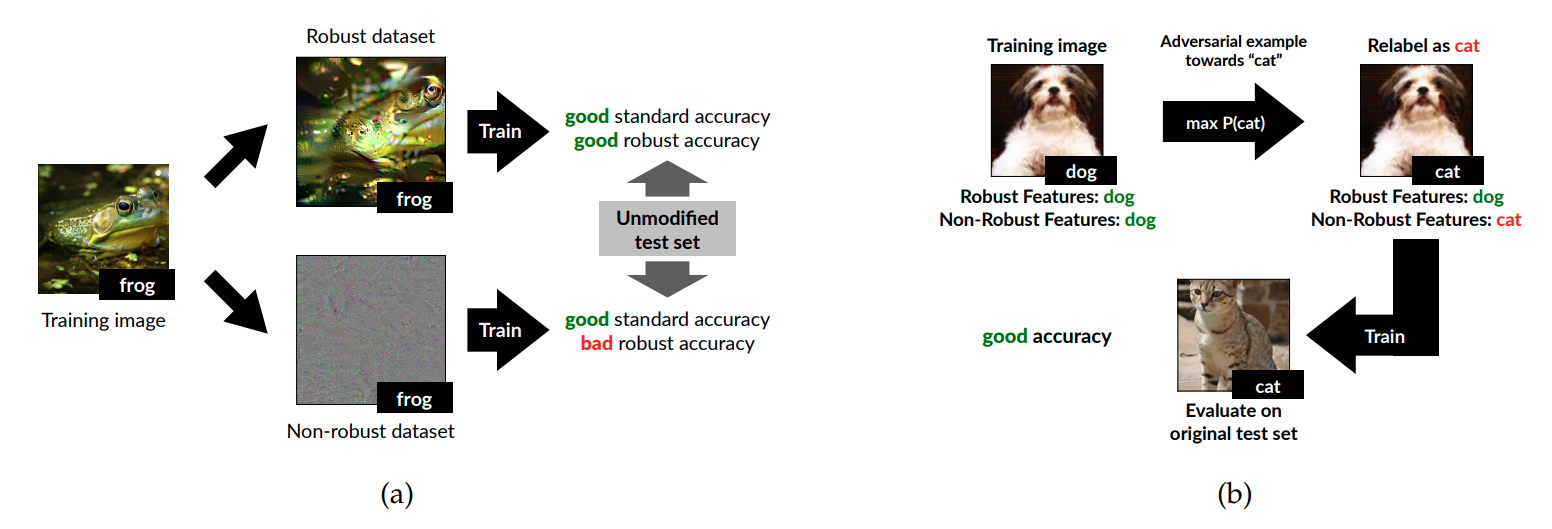
본 논문에서는 data-augmentation과 Self-supervised Multi-task learning이 유사한 성격을 지닌다고 주장하고 있다.

또한 rotation 기반으로 생각했을 때, unnecessary한 invariant 속성을 학습하기 때문에 오히려 성능이 떨어진다고 주장한다. 

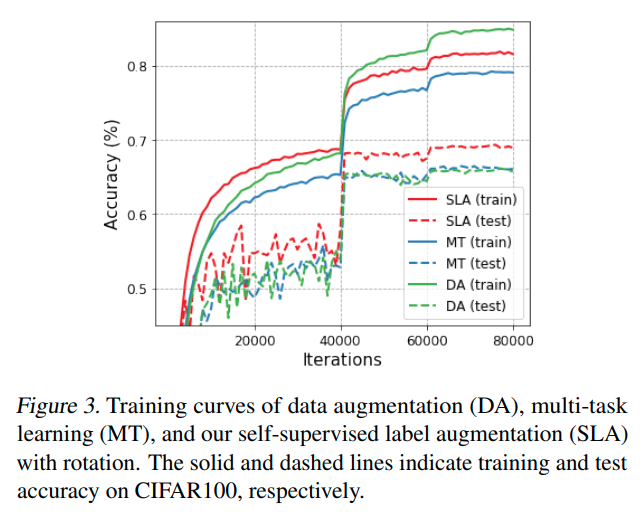
이때, test에 대해서 DA와 MT가 낮은 것은 앞선 unnecessary한 부분을 invariant하게 만들기 때문이다.

MT가 train 및 test 모두 성능이 안좋은 이유는 optimization 자체가 hard하기 때문이라고 말하고 있다.

위의 그래프에 대한 성능은 아래와 같다.  

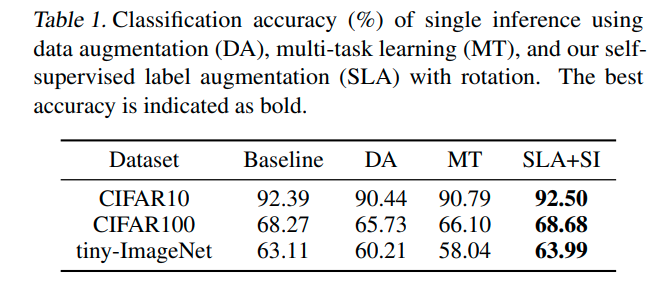
이때 DA가 Baseline보다도 성능이 낮은데, 둘의 차이는 rotation based augmentation이 있냐 없냐의 차이이다.

내 생각엔 Baseline에 다른 augmentation이 분명 포함되어 있을거라고 생각한다.

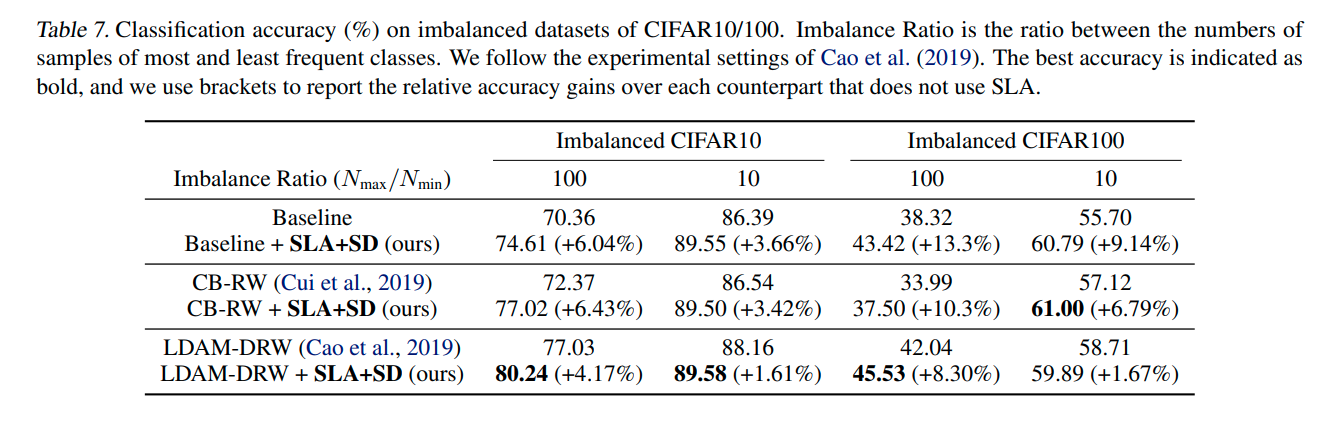
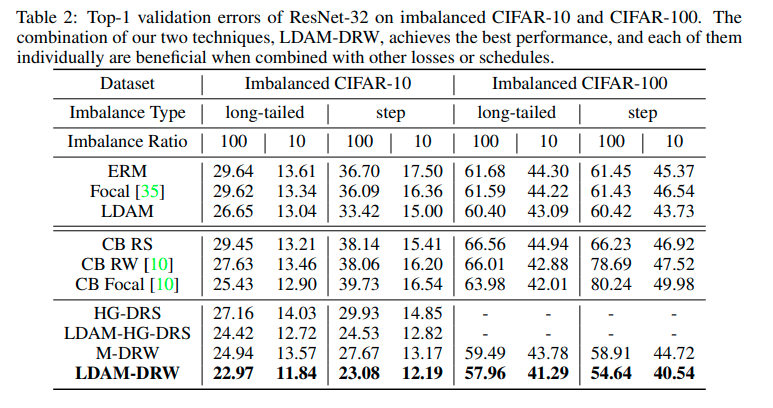
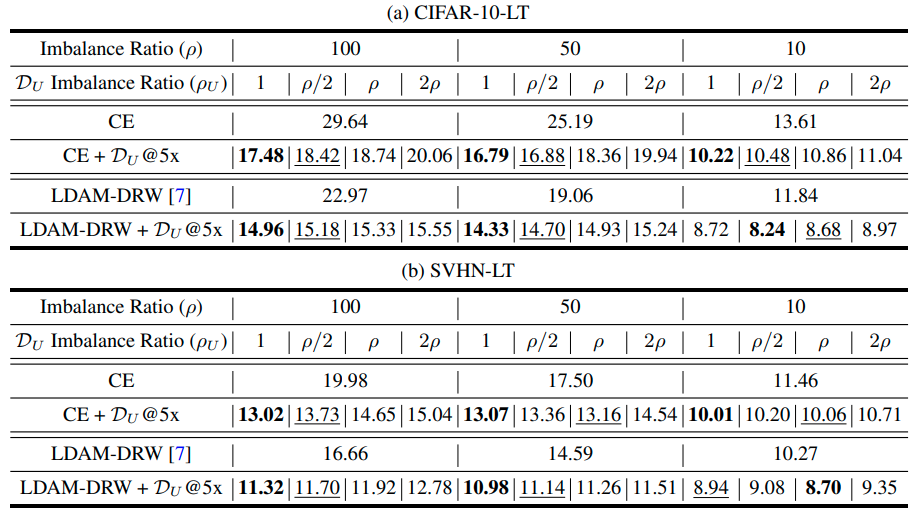
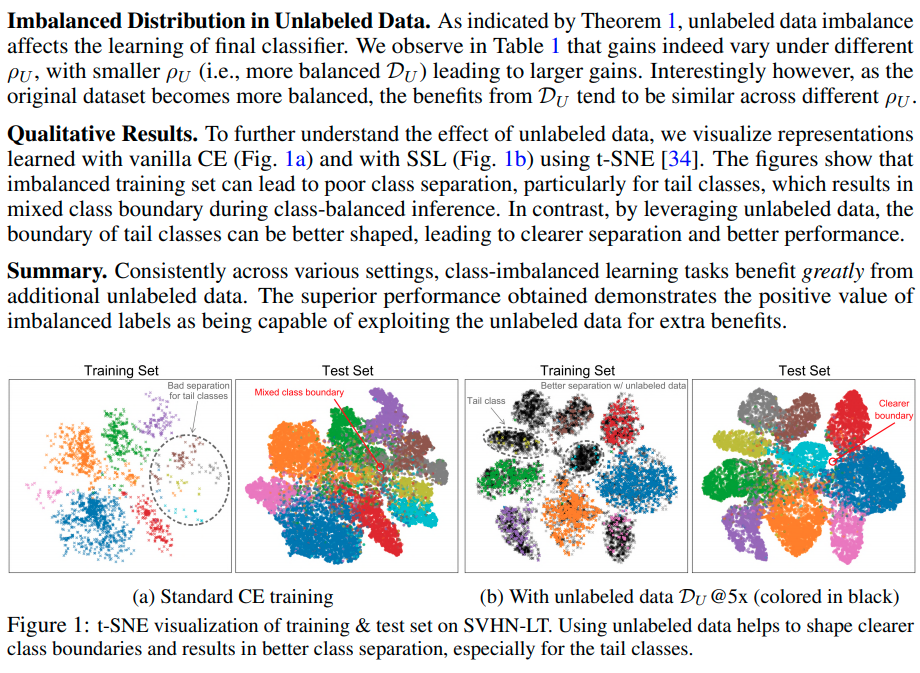
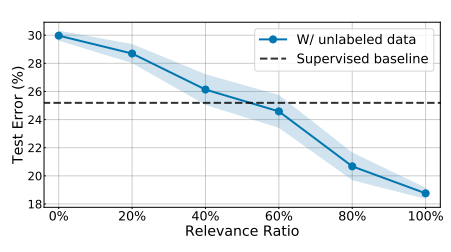
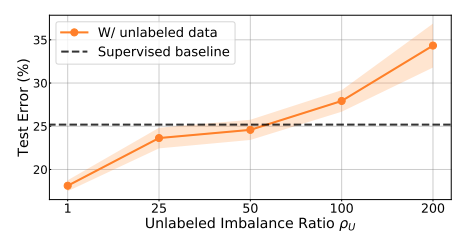
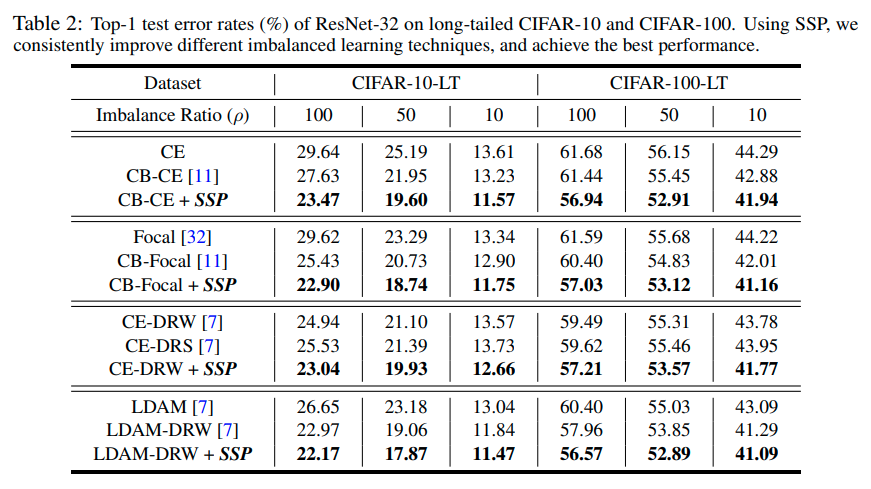
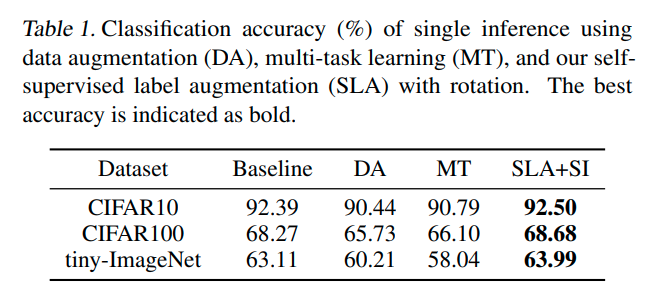
Imbalanced classification

Imbalanced classification에도 큰 성능향상을 보임 (왜?)

Paper

arxiv.org/abs/2011.00178

Introduction

대부분의 현재 classfication method들은 "What is a cat"에 집중한다. 그래서 cat의 가장 representative한 feature을 찾도록 학습한다.   본 논문에서는 "What is not a cat" 에 집중하는 학습방법을 사용한다. 그래서 non-cat data에 대한 새로운 representation Point를 찾도록 학습한다. 그리고 그것을 Reciprocal Point라고 명명한다.

그래서 본 논문에서 제안하는 method를 Reciprocal Point Learning (RPL) 이라고 한다. 

RPL은 open space risk를 줄이는 방법이다. 이때, open space란 다음과 같다.

(분모는 위의 그림 참고)

즉, embedding space에서  known data가 embedding되는 공간을 제외한 space를 open space라고 한다.

그리고 open space risk는 embedding space의 모든 공간 중에서 open space가 차지하는 비중이다.

RPL은 이 open space risk를 줄이기 위한 방법이다. 이때, known class에 대한 reciprocal point를 학습시킴으로서 open space risk를 줄일 수 있다.

상세한 과정은 다음과 같다. 

reciprocal point를  현재 학습하는  known class와 다른 extra-class를 이용해서 학습을 하고, input의 구분은 embedding feature와 reciprocal point의 차이를 이용해 구분한다.

학습과정에서는 reciprocal point를 이용해 all known class들이 reciprocal point에 push되고 pull되는 과정이 반복되게 된다. 

결과적으로 embedding space는 bounded range에 갇히게 된다.

이러한 방법을 통해 기존의 딥러닝 모델의 문제였던 unknown input에 대한 high confidcence가 나오는 문제를 boundary를 제한함으로써 해결할 수 있다.

이러한 방법으로 known sample만 traing stage때 사용할 수 있지만, reciprocal point를 이용해 known과 unknown을 분리할 수 있다.

Reciprocal Point Learning

1) Preliminaries

Open set recognition problem definition

labeled data D_L이 N known classes들과 있다고 생각해보자. 이때, 특정 category k에 해당하는 positive training data를 

특정 category k를 제외한 다른 class들에 대한 training data를 

potential unknown data를

1-class open set recognition probelm 은 다음과 같은 optimization식을 optimization 하는 것이다.

이때 R^k는 expected error이다. α는 regularization parameter이다.

R_ε 는 known data의 empirical classfication risk이다.  

R_o 는 open space risk이다.

multi class classification에서는 위와 같이 표현할 수 있다.

Reciprocal Points for Classification

category k의 reciprocal point는 다음과 같이 표현할 수 있다.

이때 M은 각 class의 reciprocal point의 수이다. 이때 P^k는 sub-dataset

k  class가 아닌 dataset 및 unknown dataset에 대한 latent representation의 set 이라고 생각될 수 있다.

이때, 특정 category k에 대해 기준으로 learninig하는 prototype or center loss와 달리,

위의 기준에 따라 reciprocal point를 설정하는 것은  S_k보다는 O_k에 있는 sample로 설정하는 것이 적절하다.

(S_k는 특정 class k의 sample이 차지하는 space, O_k는 특정 class k를 제외한 나머지 class에 대한 embedding space 및 unknown class들의 embedding space를 합친 공간이다.)

이는 다음과 같이 표현이 가능하다.

이때 ,

는 two sets의 모든 sample에 대한 distances들의 set이다.

즉 위의 식을 해석하면 다음과 같다. 

특정 class k data와 k에 대한 reciprocal point P에 대한 모든거리를 d라고 표현할때, 

class k의 reciprocal point와 class k의 제외한 데이터 및 unknown data간의 distance들의 max값을

d보다 작게 하는 것을 의미한다.

즉 한마디로 reciprocal point를 특정 class k에 대한 data들의 거리보다 k가 아닌 data들간의 거리가 가까운 점이어야 한다는 것이다.

어찌되었든 openset learning은 known space와 unknown space를 최대한 분리시키는 것이다. 

이를 위해서 class k와 reciprocal point에 대한 공간을 최대한 분리시킨다.

이를 위해서 sample x가 있고, reciprocal point P_k가 있을 때,  둘간의 거리는 sample x가 embedding 된 위치와 M개의 reciprocal point와의 distance의 평균으로 정의한다.

이때, sample x가 category k 속할 확률인 reciprocal 간의 거리에 비례하게 된다.

즉 거리가 클수록 class k에 속할 확률이 높으므로 다음과 같이 정의가 가능하다.

γ는 hyper parameter이다. γ 는 probability의 assign되는 정도를 뜻한다. (클수록 크고 급격한 확률로 속하게 됨)

Loss function은 다음과 같다.

이러한 방법을 통해 closed space와 open space의 interval을 크게 만들 수 있으며, 

또한 아래 empirical classfication risk 또한 줄일 수 있다. 

Reducing Open Space Risk

open set recognition 문제를 풀기 위해서, reciprocal loss를 open space risk를 줄이기 위해서도 같이 사용한다.

open space는 category k를 제외한 다른 class sample이 embedding되는 space

unknown sample들이 embedding되는 space

두개로 나누어 생각할 수 있다.

그러므로 모든 known class의 open space를 고려한 global open space 다음과 같다.

이때, maximum entropy 이론에 따르면, 따로 prior 조건을 주지 않은 unknown sample x_u는 

well-trained closedset disciriminant function에는 equal probability를 가지게 된다.

(최종 softmax 확률값 uniform하게 나온다.)

이것의 의미는 embedding space상에서 unknown sample은 중앙에 위치하는 경향을 가진다는 의미이다.

이는 다음과 같은 실험 결과에서 확인 가능하다.

이때, open space를 직접적으로 어떠한 공간으로 bounding 시키는 것은 어려운일이다. 왜냐하면 unknown sample의 범위가 너무나도 넓기 때문이다.

그러나 class k에 대한 space S_k와 나머지 space O_k를 상호보완적(complementary)라고 생각하면, 다음과 같이 간접적으로(indirectly) bounding이 가능하다.

이때, R_k는 learnable margin이다. 이때 위 식을 minimizing하는 것은 다음 두식을 최대한 같게 만드는 것과 같은 의미이다.

이유는 위 식에서 x의 embedding된 위치와 reciprocal point와의 거리가 바로 

이 식이기 때문이다. (집합 인 것만 다름)

그러므로 다음과 같이 된다.

위 식때문에,

와 같이 된다. (d와 R^k가 최대한 가까워지므로)

이렇게 하면 reciprocal point P_k를 중심으로 margin R^k를 가지는 boundary가 형성된다.

이 bounded space를 이용해 global unknown space를 최대한 bounded할 수 있다.

Learning Open Set Network

결론적으로 loss식은 다음과 같이 된다.

위 식의 의미는 classfication loss식에서는 k class의 reciprocal point랑 k class에 대한 sample의 거리를 크게 만드는 역할을 한다.  open space에 대한 regularization 식은 단순히 거리를 크게 만드는 것이 아니라 특정 boundary로 embedding space를 제한하는 역할을 한다.

loss 식을 통해 아래 그림과 같이 embedding space가 형성된다.

이때까지 설명한 내용을 알고리즘으로 나타내면 다음과 같다.

Experiments

RPL++은 RPL training을 위해 GCPL을 같이 사용한 경우를 말한다.

1) Experiments for Open Set Identification

2) Experiments for Open Long-Tailed Recognition

Evaluation metric

AUROC 및 AUPR을 사용, AUPR-Known과 AUPR-Unknown은 각각 known과 unknown을 positive로 놓았을때, precision-recall 값을 말한다. 

Further Analysis

1) RPL vs Softmax

Reciprocal의 classification loss term만 사용할 경우, 일반적인 cross entropy loss term과 큰 차이가 없다.

그러나 open space에 대한 loss term을 추가하는 경우, high confidence를 발생시키는 unknown sample에 대한

risk를 감소시키고 known sample이 embedding space의 중앙에 위치하여 발생하는 known sample과 unknown sample간의 overlap 또한 막을 수 있다.

2) RPL vs GCPL

GCPL경우 center loss처럼 prototype loss를 적용한 방법이다. 이러한 loss를 적용하는 경우 각 class의 sample들이 한 곳으로 뭉치는 효과가 있으나, embedding space의 주변부로 최대한 멀어지는 효과는 가지지 못한다. known class sample들을 최대한 주변부로 밀어내는 RPL에 비해 known class sample과 unknown class sample이 겹치는 것을 볼 수 있다.

3) Margin & λ.

open space loss를 λ를 통해 조절이 가능하다. 이를 통해서 margin 또한 조절이 가능하다. 

dataset 마다 적절한 margin은 다르며, 너무 작게 margin을 설정할 경우 classificaiton 성능이 떨어진다.

4) Experiments with Multiple Reciprocal Points.

Reciprocal point의 수에 대한 변화이다.

Paper

arxiv.org/abs/1905.02175

Introduction

그동안 adversarial example에 대한 여러가지 해석이 있었다.

본 논문에서는 사실 adversarial example은 deep learning model이 학습하는 featrue는

robust-feature와 non-robust feature 2가지로 나뉘게 되며,

adversarial example은 non-robust feature를 이용한 것이란 것을 증명한다.

Paper

arxiv.org/abs/2004.00431

Code

github.com/alinlab/M2m

Introduction

Imbalanced data를 다루는 방법에는 여러가지 방법이 있지만 그중에서 re-sampling 방법이 있다.

re-sampling 방법은 minority class의 sample을 생성하여, minority class의 수가 부족한 것을 해결하는 방법이다.

대표적인 re-sampling 방법으로는 SMOTE가 있다.

SMOTE는 minority class의 sampling이 feature space상에 embedding되면 sample들의 linear combination을 하여

새로운 feature space상에 sample들을 생성하는 방법이다.

그러나 minority class의 sample이 아주 작은 경우 sample을 생성하더라도 다양한 sample이 생성되지 않기 때문에,

poor performance를 보여주는 경우가 많다.

Contribution

본 논문에서는 minority sample을 생성하는 새로운 방법을 제시한다. : Major-to-minor Translation (M2m) 

기존 SMOTE 계열 방법들은 minority sample을 추가로 생성하기 위해서 minorrity class의 sample들을 이용했다.

그러나 본 논문에서는 minority sample을 생성하기 위해 majority sample을 이용한다.

M2m: Major-to-minor translation

data imbalanced 문제는 보통 다음과 같이 귀결된다.

일반적인 classification 문제는 train data distribution과 test data distribution이 동일하다고 가정한다.

그러나 imbalnced data 문제는 train data distribution과 test data distribution이 동일하지 않다. 

train data 의 경우 highly imbalanced , test data의 경우 uniform distribution을 가진다.

그래서 imbalanced된 train data를 학습하여, uniform인 test data에 잘 동작하는 것이 목표이다.

M2m method의 경우, 이를 행하기 위해 sythetic sample을 majority class로 부터 생성하여 minority sample에 추가한다. 

이러한 방법에는 image to image translation을 통한 minority image를 생성하는 방법도 존재하겠지만,

추가적인 학습 및 복잡한 방법론이다.

본 논문에서는 majority sample을 target minority sample에 대한 confidence를 maximize하는 형태로 

새롭게 minority sample을 생성한다.

이때 another baseline classifier g를 사용하는데, 이는 기존의 imblanced training data에 대해 standard ERM training을 통해 학습한 classifier이다.

때문에 classifier g는 minority class에 overfitting되어 있으며, balanced test dataset에는 generalize가 잘 되어있지는 않은 classifier이다.

이때 우리는 g를 이용해서 minority sample을 생성할 것이다. 그러므로 g는 majority class의 sample들을 이용해 minority sample들을 잘 생성할 수 있다고 가정한다.

그리고 생성된 sample들을 이용해 classifier f를 balanced testing criterion에 맞추어 새로 학습한다.

이때 g를 이용해 sample을 생성할 때, 사용하는 optimization problem 수식은 다음과 같다.

이때, L은 cross entropy loss이고, λ는 hyper parameter이다.

본 식의 의미는 다음과 같다.

major class의 sample x_0에다가 noise δ를 더해서 minority class sample x를 생성하는데,

이때, g classifier에 input으로 넣어서 target minority class k 에 대한 loss가 최소가 되도록 한다.

그리고 생성된 sample x^*를 f classifier를 학습시키는 데 이용한다. 

이때, 생성된 sample의 경우 f classifier에서 기존 class인 k_0로 분류되지 않도록 regularization term을 넣어준다.

이렇게 하는 경우, x_0에서 생성된 sample x가 f_classifier에서 기존 class인 k_0로 분류되는 것은 막으면서

x_0의 주요한 feature는 남길 수 있다고 저자는 말하고 있다. 

(f_classifier에서도 k_class로 바로 prediction하도록 optimization 수식을 세우면, 주요한 feature가 사라질 가능성 있음)

그림으로 나타내면 아래와 같다.

Underlying intuition on M2m

결론적으로 M2m은 다음 논문에서 제시한 방법을 이용한다.

-> Adversarial examples are not bugs, they are features.

결국 majority class에서 minority class에 대한 non-robust feature을 더하여 sample을 생성하는 형태이다.

Detailed components of M2m

1) Sample rejection criterion

synthetic sample을 생성할 때 중요한 것은, g classifier가 기존 class k_0에 대한 feature는 잘 제거하는 것이다.

그래야 k class의 sample을 제대로 생성했다고 판단할 수 있기 때문이다. 

그러나 g classifier는 완벽하지 않기 때문에, k_0를 이용해 k class의 sample을 완벽하게 생성하지는 못한다.

그러므로 생성된 sample이 오히려 방해가 될 가능성이 있다. 

(k_0에 대한 diciriminative한 feature가 남아있을 가능성이 있음)

이러한 risk는 특히 생성을 위해 사용하는 k_0의 sample수가 작을 경우 더 심해진다. 

이러한 risk를 줄이기 위해서 저자는 synthetic sample을 일정 확률로 rejecting하는 방식을 제안한다.

위 식의 의미는 N_k_0 - N_k의 max 값을 B의 exponential 값으로 이용하겠다는 것이며,

B의 값이 작을수록 classifier g의 reliability가 더 높다는 것을 의미한다.

예를 들어 B=0.999이면, sample을 accepted하는 probability가 N_k_0 - N_k > 4602일때, 99% 이상이다.

B=0.9999이면, N_k_0 - N_k > 4602일때 99% 이상이다. 

이러한 모델링은 effective number 논문에서 참고한것이다.

위 논문에서, larger dataset에서 sample이 하나 추가될 경우 실제로 적용되는 효과는 exponentially하게 decrease된다고 한다.

(그냥 확률적으로 rejection 한다는 것이 불분명함)

만약 synthetic sample이 reject되는 경우, original dataset에 있는  minority sample을 대신 추가해준다.

2) Optimal seed sampling

그 다음 고려해볼만한 사항은 class k_0에 대한 majority seed sample x_0를 어떻게 선정할 것인가에 대한 내용이다.

이를 위해서 저자는 다음과 같은 Q(k_0 | k) 를 design 했다.

이때 2가지를 고려한다.

(a) Q는 acceptance probability P_accept(k0_|k)를 maximize 하도록 정한다.

(b) Q는 가능한 diverse class를 정하도록 한다. 즉 entropy H(Q)를 maximize하도록 한다.

결국 다음과 같이 식을 세울 수 있다.

이 optimization을 최대화하는 Q는 P_accept이다. (why?)

그래서 Q(k_0|k)는 다음과 같다.

위의 Q를 이용해 k_0가 결정되면 x_0는 uniform하게 random sampling 한다.

전 과정을 나타내면 다음과 같다.

Paper

arxiv.org/abs/1901.05555

Code

github.com/vandit15/Class-balanced-loss-pytorch

Introduction

imbalanced-data 문제에서는 re-sampling, re-weighting 방법이 주로 적용된다. 

이러한 방법은 주로 class frequency의 inverse하게 weighting을 적용했었다.

그러나 최근 연구에서 이러한 방법이 poor performance를 보였었고, 

때문에 square root에 inverse 하여 weighting 하는 smoothed version이 제안되었다.

이러한 발견은 다음과 같은 의문을 낳게 되었다.

"다양한 imbalanced data에 따라 어떻게 class balanced weighting을 하는 것이 좋은 것일까?"

위 그림과 같이 highly imbalanced data에 바로 sample 수에 inverse하게 re-weighting 방법을 적용하는 것은 좋은 성능을 내지 못한다. 

일반적으로 생각하기에는 data가 많을 수록 성능이 좋아지는 것이 맞지만, 비슷한 data가 추가되는 경우, 실제로 반영되는 효과는 낮다. 그렇기 때문에 각 class마다 'effective number'를 구하고 effective number를 기준으로 하여 re-weighting을 진행한다.

그래서 이 논문의 main contribution은 다음과 같다.

(1) long-tailed dataset을 다루기위한 effective number of sample의 이론적 분석 및 loss function에 적용하는 class balanced term을 design

(2) class balanced term을 기존의 loss function에 추가함으로써, 높은 성능 향상을 가져옴 (cross entropy, focal loss) 

Effective Number of Samples

1) Data Sampling as Random Covering

먼저 sample들의 effective number를 E_n으로 정의한다. 이때 n은 sampling된 example의 수이다.

수학적으로 너무 복잡해지는 것을 막기 위해 partially overlapped 되는 상황은 제외한다.

기존에 있던 data와 overlapped 되는 확률을 p, overlapped 되지 않는 경우를 1-p로 정의하며,

sampling을 진행할 수록 overlapped 될 확률이 커지기 때문에 p는 커지게 된다.

이때, effective number를 수식으로 나타내면 다음과 같다.

이 수식을 증명하는 과정은 다음과 같다.

먼저 E_1=1이다.  (sample이 단 하나이므로 overlapping이 전혀 이루어지지 않기 때문에 당연한 결과이다.)

그러므로 다음과 같이 수식을 먼저 쓸 수 있다.

그리고 n-1개의 example을 sample하고 n번째 example을 sampling하는 경우를 생각해보자.

n-1개의 sample을 sampling했을 때, expected volume은 E_n-1이 된다. 이때, 새롭게 sample된 데이터가 

overlapped될 확률은 다음과 같다.

그러므로 n번째 example이 sampling되었을 때, expected volume은 

와 같이 된다.

이때, E_n-1을 다음과 같이 가정하면

즉, 처음에 가정했던 식이 맞게 된다. (점화식 형태)

이는 samples의 effective number가 n의 exponential function이라는 것을 알려준다.

B는 0~1사이의 값을 가진다. E_n을 다른 형태로 표현하면 다음과 같다.

이 수식의 의미는 j번째 sample이 effective number에 영향을 주는 정도가 B^(j-1)이라는 것이다.

그래서 all possible data의 total volume은 다음과 같이 계산이 가능하다.

위 식을 토대로 다음과 같은 점근적 성질을 발견할 수 있다.

내용을 해석하면, all possible data N이 커질수록, effectve number of sample의 값은, 실제로 sampling된 숫자 n과 같게 된다.

즉, N이 커질수록 data overlap이 사라지고, 모든 sample이 unique해진다는 것을 의미하며, N=1인 경우는 오직 하나의 prototype만 존재하는 상황을 의미한다.

Class-Balanced Loss

input sample을 x , label을

라고 정의하자. 이때 model이 각 class에 대해 prediction한 probability를 다음과 같이 정의한다.

위의 정의에 따라 loss를 L(p,y) , class i의 number of samples를 n_i라고 하자.

그러면 effective number of samples for class를 다음과 같이 나타낼 수 있다.

이때, N_i 를 특정하게 좋은 값으로 설정하는 건 어려운 일이기 때문에 다음과 같이 dataset에 맞게 설정한다.

class-balanced loss를 적용하기 위해서 weighting vector a를 적용한다. 

이때 weighting은 class i에 대한 effective number of samples에 inverse하게 적용한다.

weighting을 적용했을 loss값의 scale이 달라지기 때문에 아래 식으로 나눠줌으로써, 다시 normalize해준다.

결론적으로 본 논문에서 제시하는 CB (class-balanced) loss는 다음과 같다.

이 loss function을 B를 변화시키며 나타내면 다음과 같다.

B가 1에 가까워질수록 inverse class frequncy에 맞게 re-weighting 된 것을 의미한다.

이러한 class-balanced loss는 모델이나 loss function에 general하게 적용이 가능한 장점이 있다.

본 논문에는 이를 증명하기 위해서 softmax cross-entropy loss, sigmoid cross-entropy loss, focal loss에 적용하였다.

Class-Balanced Softmax Cross-Entropy Loss

Class-Balanced Sigmoid Cross-Entropy Loss

Class-Balanced Focal Loss

Experiments

Imbalance factor는 가장 sample수가 많은 class의 sample 수와 가장 sample수가 작은 class의 sample을 나눈 값이다.

Paper :arxiv.org/abs/1911.05722

Code :github.com/facebookresearch/moco

Introduction

MoCo는 Contrasive learning 기반 unsupervised learninig method로서 contrasive learning 적용을 위한 'key' sample을 queue형태로 구성하고, key sample 용도의 encoder를 moving average 형태로 update하는 방식이다.

그래서 아래와 같은 형태를 띈다.

기존의 contrasive learning과 가장 크게 다른 점은 key sample들을 queue형태로 저장한다는 점이다.

그래서 현재의 mini-batch에 있는 sample들은 encoding되어 enqueue되면, oldest는 dequeue된다.

이러한 queue memory를 사용하는 경우, dictionary size를 mini-batch size 이상으로 크게 키울 수 있다는 장점이 있다.

게다가 이전의 key를 저장하고 사용할 수 있기 때문에, key encoder의 변화를 'slowly progressing' 할 수 있다. 

이러한 방법을 통해 key encoder가 생성하는 feature의 consistency를 유지할 수 있다.

Contrastive Learning as Dictionary Look-up

Contrasive loss는 다음과 같이 정의된다.

먼저 encoded q와 encoded sample 모음인 dictionary {k0 , k1, k2....} 가 있다고 생각해보자.

이때, dictionary안에 q와 같은 positive sample이 하나 있다고 가정하고 그것을 k+라고 한다.

그리고 나머지는 negative sample이라고 생각하자.

이때 , Loss는 다음 식으로 표현된다.

Momentum Contrast

위의 시각에서 볼때, contrasive learning은 high dimensional space에 discrete dictionary 를 쌓는 과정과 같다.

이때, key가 randomly 하게 sampled 되는 것을 볼때, dictionary 는 'dynamic'하다고 표현할 수 있다.

그리고 key encoder는 training을 거치면서 학습이 되게 된다.

이때, key encoder가 good feature를 학습하기 위해서는 어떻게 해야 될지 고민했고, 다음과 같은 가설을 세우게 된다.

1. good feature는 'large' dictionary로 부터 배울 수 있다. (많은 negative sample이 있으므로, queue를 쓰는 이유)

2. 그러나 encoder를 위한 dictionary key는 가능한 consistent하게 유지될 수 있어야 한다.  (encoder가 학습이 진행되더라도)

이러한 가설 아래 저자들은 Momentum Contrast를 제안한다.

Dictionary as a queue.

저자가 제안한 아이디어의 핵심 중 하나는 key 값들을 저장하는 dictionary를 queue로서 구성하는 것이다.

이러한 접근 방식은 이전 mini-batch에서 encoding되었든 key를 다시 사용할 수 있다는 장점이 있다.

즉, dictionary의 size를 minibatch size의 한계에서 벗어나게 하는 장점이 있는 것이다.

 또한 이는 hyperparameter로서 조정이 가능하다.

이떄, dictionary에 있는 sample들은 계속해서 update된다.

current minibatch가 dictionary에 enque되면, queue에 있는 oldest mini-batch가 제거된다.

그래서 dictionary는 모든 data의 subset로서 구성된다.

Momentum update

queue를 사용하는 것은 dictionary size를 크게하는 장점이 있지만, back-propagation에 의해서 key encoder를 dictionary 안에 있는 모든 sample에 대해서 계산하여 update하기는 불가능하다는 단점이 있다. (이해 제대로 못했음)

이러한 문제점을 해결하기 위한 간단한 방법은 query encoder를 key encoder로 copy하는 형식으로 update하는 것이다.

그러나 실험 결과가 좋지 않았다.

저자들은 이러한 방식이 key representation의 consistency를 너무 빠르게 변화시키기 때문이라고 가정한다.

그래서 momentum update를 적용한다.

이때, key parameter는 back propagation으로 update되지 않고, query encoder만 update된다. 

위 식에 의해서 key encoder는 query encoder에 비해서 더 천천히 update되는 효과를 가져다 준다.

이러한 방법을 통해 queue에 있는 key들은 different encoder에 의해서 encoding이 되지만, 

2개의 encoder에 의해서 encoding된 결과의 차이는 줄어들게 된다.

실험결과에 따르면 momentum value가 클수록 더 좋은 결과가 나왔다. (m=0.999 > m=0.9)

Shuffling BN

f_q , f_k  모델 둘다 batch normalization을 사용하는데, 실험결과 BN이 good representation을 학습하는데 오히려 방해가 됨을 확인하였다. BN 과정에서 생기는 batch 내부 안의 정보 공유가 학습을 방해하는 것으로 추측하고 있다.

그리고 저자들은 이 문제를 shuffling BN으로 해결하고 있다.

key encoder f_k 에 대해서 mini-batch의 sample order를 shuffle한다. 그리고 GPU로 전달한다. 

그리고 encoding이 끝나면 shuffle 된 것을 다시 되돌린다.

그리고 query encoder f_q의 sample order는 변경하지 않는다.

즉, query와 positive key가 다른 batch상에서 나와야 하며, 같은 batch에 있는 경우 batch normalization 계산과정에서

정보를 공유하는 부분 때문에 더 좋은 representation 학습에 방해가 된다.

Paper

arxiv.org/abs/1906.07413

Code

github.com/kaidic/LDAM-DRW

Introduction

Imbalanced data 문제는 보통 re-weighting, re-sampling 접근 방법을 많이 사용한다. 이는 train data distribution과 test data distribution을 동일하게 만듬으로써, 문제를 접근한다. 하지만 결국 minority class의 sample의 부족은 overfitting을 발생시킨다는 것은 큰 어려움이다.

그래서 저자는 majority class에 비해 minority class에 강한 regularizing 기법을 적용함으로써, minority class에 대한 정확도를 향상시키는 방법을 제안한다. 

이는 기존의 weight matrix에만 regularization 방법을 적용한 것과 달리, label에도 함께 regularization 방법을 적용한다.

결론적으로 본 논문에서는 label-distribution-aware loss function을 적용함으로써, model의 margin을 minority class에 대해 좀 더 크게 되도록 최적화한다.

Main approach

1) Problem setup and notations

2) Fine-grained generalization error bounds.

일반적인 generalization error bound는 다음과 같다. (training , test data distribution이 동일한 경우)

이는 모델의 복잡도가 증가할수록 overfitiing이 잘되기 때문에, 복잡도에 비례하게 되고, training data 수가 많을수록 

실제 data의 분포에 맞게 학습이 가능하기 때문에 error bound가 작아지게 된다.

그리고 training, test 모두 동일하게 imbalanced distribution인 경우, error bound는 다음과 같이 형성된다.

위의 식의 의미는 class간의 margin중에서도 최소값인 r_min이 크다는 것은 class 간의 boundary가 잘 형성되어있다는 의미이고, error의 최대값이 작아진다는 의미이다.

그러나 위 식에서는 label distribution에 대한 정보는 나타나 있지 않다.(oblivious)

그래서 다음과 같이 fine-grained하여 loss function을 다시 구성한다.

3) Class-distribution-aware margin trade-off

위의 margin 식을 살펴보면 class에 대한 sample의 수가 많을수록 error bound가 작아지는 것을 확인할 수 있다.

즉, minority class에 대한 error bound를 줄이려면 margin값을 크게 해야한다는 사실을 알 수 있다.

그러나 minority class에 대해 margin을 너무 크게 하면, majority class에 margin이 작아지는 단점이 있다.

그렇다면 optimal한 margin은 어떻게 구할 수 있을까?

class가 2개인 binary classfication 문제인 경우 balancd generalization error bound를 다음과 같이 나타낼 수 있다.

( 5번식 참고)

이때, r_1과 r_2는 복잡한 weight matrices이기 때문에 optimal margin을 구하기 어렵다.

하지만 이러한 방식으로 접근이 가능하다. 만약 margin r_1, r_2가 현재 optimal이라면,

shifted bias를 현재 margin에 적용했을때, 아래와 같이 error bound가 더 커져야 한다.

위 식은 다음과 같은 의미를 내포한다.

4) Fast rate vs slow rate, and the implication on the choice of margins.

generalization error bound에는 Fast rate와 slow rate라는 용어가 있다.

의 scale에 따라 bound가 변화하는 경우, 'slow rate'라고 부른다.

위와 같이 변화하는 경우 'fast rate'라고 부른다.

딥뉴럴넷이 충분히 큰 경우 위와 같이 fast rate로 바뀔 수 있다.

Label-Distribution-Aware Margin Loss

위의 binary classificaiton의 경우를 고려하여 저자는 multiple case에 대해서 다음과 같이 가정한다.

그리고 soft margin loss function을 위와 같은 margin을 가지도록 디자인한다. (optimal margin이므로)

(x,y)를 training example이라고 하고, f를 모델이라고 하자. 이때, 

를 model의 j class에 대한 output이라고 정의한다.

이때 hinge loss를 이용해서 

위와 같이 loss function을 구성가능하다.

위 식의 의미는 다음과 같다. label y에 대한 logit과 다른 클래스 logit의 max값의 차이가 최소 △는 되어야 한다.

그러나 hinge loss가 smooth 하지 않은 점은 optimization 과정에서 문제점을 만들어내고, 다음과 같이 cross-entropy loss에 margin을 부여해서 smooth한 hinge loss를 만들어 낼 수 있다.

label y에 대한 logit이 margin보다 커야 loss값을 줄일 수 있음

Deferred Re-balancing Optimization Schedule

re-weighting 방법과 re-sampling 방법은 imblanced dataset을 다루는 주요한 방법이다.

(둘다 uniform한 test distribution에 가깝게 만드는 방법이기 때문)

그러나 re-sampling 방법의 경우 model이 deep neural network인 경우 heavy overfitting이 나타난다고 알려져 있다.

그리고 re-weighting의 경우 optimazation이 불안정하다는 단점이 있다. (특히 extremely imbalanced인 경우)

그래서 이전 연구에서 이러한 optimization 문제를 다루기 위해 복잡한 learninig rate schedule을 적용한 바가 있다.

저자들은 re-weighting , re-sampling 방법 모두다 learning rate를 적절히 annealing 하지 않는 경우, 

ERM보다 오히려 성능이 떨어지는 것을 발견하였다. (all training example에 대해 똑같은 weight를 주는 방법)

annealing을 하기 전에 re-sampling 및 re-weighting 방법으로 생성된 feature의 경우 오히려 안좋은 것으로 확인되었다.

그래서 다음과 같은 defered re-balancing training procedure를 만들었다.

먼저 LDAM loss를 vanila ERM (no weighting) 방법을 사용하여 training 시킨다. 그리고 이후에 smaller learinig rate를 이용해 re-weight LDAM loss를 적용한다. 실험 결과적으로 training의 first stage(no weighting) 는 second stage(weighting)의 좋은 초기화 방법이 된다. 

Experiments

1) Baselines

(1) ERM loss : 모든 example에 대해서 똑같은 weight를 적용한 방법, standard cross-entropy loss를 사용한다.

(2) Re-Weighting(RW) :  class의 sample size에 inverse하게 weighting한다. 

(3) Re-Sampling(RS) : 각 example을 sampling할때, class sample size에 inverse하게 sampling

(4) CB : Class-balanced loss based on effective number of samples 논문 참고

(5) Focal Loss : Focal loss for dense object detection.  논문 참고

(6) SGD schedule : SGD를 learning rate dacay method 방법을 사용한 것. 

2) Our proposed algorithm and variants.

(1) DRW and DRS : 먼저 Algorithm 1에 적힌 것 처럼 standard ERM optimization을 적용하고 그 다음 second stage때 re-weighting 및 re-sampling 방법을 적용하는 것을 말한다.

(2) LDAM : 본 논문에서 제안된 Loss function을 적용한 것.

3) Experimental results on CIFAR

HG-DRS 는 Hinge Loss+DRS

LDAM-HG-DRS는 Hinge Loss에 LDAM margin을 준 것,

M-DRW는 cross-enropy에 uniform margin을 줘서 사용한 것을 말한다.

Hinge Loss의 경우 100 class에서 optimization 이슈가 있어서 10개 클래스에서만 실험하였다.

Conclusion

1) LDAM loss를 통해 최적화 된 class 별 margn을 찾음 (binary를 통한 추론값을  multi class에 적용

2) 학습 초반 부터 re-weighting 및 re-sampling 기법을 적용하면 feature의 학습이 저해되는 부작용이 있는데,

    처음에는 standard training 방법을 사용하고 이후에 re-weighting 및 re-samping을 적용하는 deferring 방법을 사용함.

Paper

arxiv.org/abs/2006.07529

Code

github.com/YyzHarry/imbalanced-semi-self

Introduction

일반적인 supervised learning에서는 data의 label은 무조건 도움이 된다.

unsupervised learning과 비교해보면 그것을 알 것이다.

그러나 imbalanced learning에서는 상황이 달라진다.

majority class에 의해 decision boudary가 강하게 형성되게 되고,

아래와 같이 decision boudary가 형성되는 경향성을 보이게 된다. 

그래서 다음과 같은 의문을 제기 한다.

그래서 본 논문에서는 imblanced learning에서의 label의 positive한 면과 negative한 면을 살펴보고 이를 semi-supervised learning과 self-supervised learning 방식으로 이용하여 sota를 달성했다.

먼저 positive view는 imbalanced label이 유용하다는 것이다. 그래서 extra unlabeled data를 추가적으로 사용하여 psedo-labeling data를 형성하고 이를 통해 semi-supervised 방식으로 추가적인 학습을 진행하면, imblanced data 학습을 통한 성능이 향상된다는 것을 증명하고 있다.

그리고 negative view는 imbalanced label이 항상 유용하지는 않다는 것이다. imbalanced label만을 이용해 학습할 경우 acc의 최대치의 bound가 정해지게 된다.  그러나 label을 따로 지정하지 않는 self-supervised 방식을 적용하면 imbalanced label만을 이용해 학습할 경우 제한되는 acc의 한계를 넘을 수 있다는 것이다. 본 논문에서는 이를 수식 및 실험적으로 증명하고 있다.

Imbalanced Learning with Unlabeled Data 

먼저 Unlabel Data를 추가적으로 학습에 사용할 때, 어떠한 효과가 있는지 알아보기 위해 이론적으로 살펴본다.

먼저 binary classification 문제를 고려한다. data는 2개의 Gausssian의 mixture P_xy 모델을 사용한다. 

label Y는 positive value (+1) , negative value (-1) 2가지를 같은 확률 (0.5)의 확률로 가지게 된다.

그래서 Y=+1 일때, data X의 label이 +1 인 경우는 다음과 같이 normal distribution을 따른다. ( label 1에 대한 u_1 gaussian)

Y= -1 일때, data X의 label이 -1 인 경우는  다음과 같이 normal distribution을 따른다. ( label 2에 대한 u_2 gaussian)

이 경우 optimal bayes's classifier는 

가 된다.

이 경우, 

가 된다.

이러한 상황에서 base classifier f_b를 정의해보자. (which is trained on imbalanced training data)

그리고 extra unlabeled data

가 주어졌다고 생각해보자.

base classifer f_B를 이용해 unlabeled data에 대해서 psuedo-label을 형성한다.

결과적으로 psuedo-label이 +1인 unlabeled-data set을  

psuedo-label이 -1인 unlabeled -dataset을

로 표시한다.

이때, psuedo-label이 +1로 분류된 data가 실제로 label이 +1인 경우 indicator를 사용해 '1'로 표시해준다.

그래서,

이때 

가 되고, 의미는 f_B가 Positive class에 대하여 p의 acc를 가진다는 의미이다.

유사하게

가 되고, 의미는 f_B가 Negative class에 대하여 q의 acc를 가진다는 의미이다.

결과적으로

로 정의가능하다.

이러한 상황에서, extra unlabeled data를 이용해,

를 배우는 것이 목표이다.

저 parameter를 측정하는 방법은 아래와 같이 측정이 가능하다.

이때 다음과 같은 결과를 얻을 수 있다.

이 결과는 다음과 같이 해석할 수 있다.

1) Training data imabalance를 estimation의 정확도에 영향을 준다.

위 수식을 보면 △ 가 estimation에 영향을 주는 것을 확인 할 수 있다. 즉, imbalance 정도가 estimation에 영향을 준다.

2) unlabeled data의 imbalanced 정도는 good estimation을 얻을 확률에 영향을 준다.

이때, unlabeled data가 balanced인 경우 good estimation을 확률이 증가한다.

그러나 unlabeled data가 balanced하지 않더라도 어찌되었든 imbalanced data를 추론하는 것에는 도움이 된다.

Semi-Supervised Imbalanced Learning Framework

이러한 가설을 기반으로 본 논문에서는 "Semi-Supervised Imbalanced Learning Framework"를 제안한다.

먼저 original imbalanced dataset 으로 부터 학습시킨 intermediate classifier 'f' 를 얻는다.

그리고 이 'f'를 이용하여 unlabeled data D_u로 부터 pseudo-label y를 생성한다. 

이를 이용하여 최종 모델 f는 다음과 같은 Loss식을 이용해 얻는다.

여기서 w는 unlabels weight이다. 

이 방식은 다른 어떠한 SSL 방식에도 적용이 가능하기 때문에 더욱 실용적이다.

Experimental Setup

실험은 2가지 dataset에서 진행되었다.

CIFAR-10, SVHN

CIFAR-10의 경우 CIFAR-10에 유사한 Tiny-imagenet class data를 unlabel data로 사용한다.

SVHN의 경우 extra SVHN dataset을 unlabeled dataset으로 사용한다.

Why good?

이건 SSL을 좀 더 이해해야 될듯

Experiment results

A Closer Look at Unlabeled Data under Class Imbalance

이러한 SSL 방식을 통해 unlabel data를 이용하는 방법은 unlabel data와 original data의 distribution match가 잘맞는 것이 중요하다.

- Data relevance가 낮으면 성능에 저해가 된다. 기준은 Relevance ratio 60% 이다.

Imbalanced Learning from Self-Supervision

Imbalaced data의 label은 어찌되었든 bias를 가지고 있기 때문에 classification 성능에 악영향을 끼치게 된다.

따라서 본 논문에서는 label을 따로 지정하지 않는 self-supervision 방식을 도입하여 성능 향상이 가능함을 보여준다.

먼저 이론적으로 self supervision이 도움이 되는 것을 증명하기 위해 다음과 같은 상황을 가정한다.

d-dimension binary classification, data distribution P_xy  mixture Gaussian을 가정한다.

이때, Y=+1은 prob p_+ 를 가지고, Y=-1은 prob p_-를 가진다. (p_- = 1-p_+) 그리고 p_-는 0.5보다 큰 것을 가정한다.

(major class를 negative로 정의하기 때문임)

Y= +1, X는 d-dimensional isotropic Gaussian이라고 정의할 경우, 

이유는 negative sample이 더 큰 variance를 갖기 때문이다. 

(majority class는 sample수가 많고 그 이유 때문에 큰 variance를 갖는다.)

이 상황에서  self-supervision을 적용하기 전과 적용한 후를 비교하기 위해 linear classifier에 self-supervision을 적용하기 전과 후를 비교할 예정이다.

linear classifier를 

여기서 'feature'는 standard training을 통해 배우는 feature이다.

self-supervised learning을 통해 배우는 feature는 다음과 같이 표현한다.

이때 다음과 같은 결과를 도출할 수 있다.

Theorem 2는 standard training으로는 3/4이상의 acc를 가지지 못한다는 것을 이야기 한다. (B가 3일때)

그러나 self-supervision을 통해 Z를 추출하면 더 높은 정확도를 얻을 수 있다.

위의 내용은 다음과 같은 내용을 의미한다.

처음에 imbalanced dataset의 label을 제거한 후, self-supervised 방법을 통해 f_ss 를 만든 후 imblanced learning을 하는 경우 더 좋은 성능을 보이게 된다.

Self-Supervised Imbalanced Learning Framework

SSP 를 적용하는 방식은 다음과 같다. 먼저 self-supervision 방식을 통해 f를 학습시킨 후, standard training 방식을 적용하여 final model을 만든다. 이러한 방식은 어떠한 imbalanced learning method에 적용이 가능하기 때문에 장점이 있다.

Experimental Setup

RotNet이랑 MoCo를 사용함.

학습은 pretrain, standard train 모두 같은 epoch 적용 (CIFAR-LT 200 epoch , ImageNet-LT 90 epoch)

results